练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】李先生的网店经营坚果类食品，一年中各月份的收入、支出（单位：百元）情况的统计如图所示，下列说法中错误的是（ ）

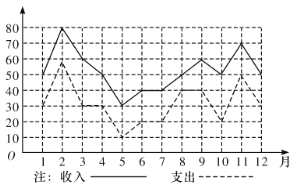
    A. 2至3月份的收入的变化率与11至12月份的收入的变化率相同

    B. 支出最高值与支出最低值的比是

    C. 第三季度平均收入为5000元

    D. 利润最高的月份是2月份

    【答案】D

    【解析】

    通过图表信息直接观察，计算，找出答案即可．

    解：A，2至3月份的收入的变化率为20，11至12月份的变化率为20，故相同．A正确．

    B，支出最高值是2月份60百元，支出最低值是5月份的10百元，故支出最高值与支出最低值的比是6：1．故B正确．

    C，第三季度的7，8，9月每个月的收入分别为40百元，50百元，60百元，故第三季度的平均收入为50百元，故C正确．

    D，利润最高的月份是3月份和10月份都是30百元，高于2月份的利润是80﹣60＝20百元，故D错误．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对在直角坐标系的第一象限内的任意两点，作如下定义:,那么称点是点的“上位点”，同时点是点的“下位点”.

    （1）试写出点的一个“上位点”坐标和一个“下位点”坐标；

    （2）设、、、均为正数，且点是点的上位点，请判断点是否既是点的“下位点”又是点的“上位点”，如果是请证明，如果不是请说明理由；

    （3）设正整数满足以下条件：对任意实数，总存在，使得点既是点的“下位点”，又是点的“上位点”，求正整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等差数列的公差,前项和为,且满足,

    （1）试寻找一个等差数列和一个非负常数,使得等式对于任意的正整数恒成立,并说明你的理由；

    （2）对于（1）中的等差数列和非负常数,试求（）的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为平行四边形，已知，，于.

    （1）求证：；

    （2）若平面平面，且，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

    （Ⅰ）证明MN∥平面PAB;

    （Ⅱ）求直线AN与平面PMN所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中， 与相交于点，点在线段上，，且平面．

    （1）求实数的值；

    （2）若，, 求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市为了解社区群众体育活动的开展情况，拟采用分层抽样的方法从A,B,C三个行政区抽出6个社区进行调查.已知A，B，C行政区中分别有12，18，6个社区.

    （1）求从A,B,C三个行政区中分别抽取的社区个数；

    （2）若从抽得的6个社区中随机的抽取2个进行调查结果的对比，求抽取的2个社区中至少有一个来自A行政区的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为评估设备生产某种零件的性能，从设备生产零件的流水线上随机抽取100件零件作为样本，测量其直径后，整理得到下表：

    直径

    58

    59

    61

    62

    63

    64

    65

    66

    67

    68

    69

    70

    71

    73

    合计

    件数

    1

    1

    3

    5

    6

    19

    33

    18

    4

    4

    2

    1

    2

    1

    100

    经计算，样本的平均值，标准差，以频率值作为概率的估计值，用样本估计总体.

    （1）将直径小于等于或直径大于的零件认为是次品，从设备的生产流水线上随意抽取3个零件，计算其中次品个数的数学期望；

    （2）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为，并根据以下不等式进行评判（表示相应事件的概率）：①；②；③.评判规则为：若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙；若仅满足其中一个，则等级为丙；若全部不满足，则等级为丁，试判断设备的性能等级并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：，过焦点F的直线l与抛物线C交于M，N两点.

    （1）若直线l的倾斜角为，求的长；

    （2）设M在准线上的射影为A，求证：A，O，N三点共线（O为坐标原点）.

    查看答案和解析>>

    同步练习册答案