
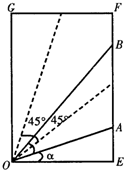
 如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=
如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=| 3 |
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| ||||
2cos(2α+
|
| 1 |
| 2 |
| 3 |
| π |
| 12 |
| π |
| 4 |
| ||||
2cos(2α-
|
| 6 |
| 3 |
| ||
| 2 |
 解:(1)∵OE=1,EF=
解:(1)∵OE=1,EF=| 3 |
| π |
| 12 |
| 1 |
| 2 |
| sin45° |
| 2cosα•cos(45°+α) |
| ||
2cos(2α+45°)+
|
| π |
| 12 |
| π |
| 4 |
| 1 |
| cosα |
| ||
| cos(45°-α) |
| 1 |
| 2 |
| 1 |
| 2cosα |
| ||
| cos(45°-α) |
| ||||
2cos(
|
|
| π |
| 12 |
| ||||
2cos(2α+
|
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 12 |
| 3 |
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| π |
| 4 |
| π |
| 4 |
| ||||
2cos(2α-
|
| 6 |
| 3 |
| ||
| 2 |
| π |
| 8 |
| 6 |
| 3 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
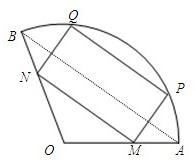 如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2013年浙江省温州市高一摇篮杯数学竞赛模拟试卷(二)(解析版) 题型:解答题
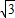 ,设∠AOE=α.
,设∠AOE=α.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年宁夏银川一中高一(下)期末数学试卷(解析版) 题型:解答题
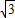 ,设∠AOE=α.
,设∠AOE=α.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com