【题目】给出下列四个命题：
①线性相关系数r的绝对值越大，两个变量的线性相关性越弱；反之，线性相关性越强；
②将一组数据中的每个数据都加上或减去同一个常数后，平均值不变
③将一组数据中的每个数据都加上或减去同一个常数后，方差不变
④在回归方程
＝4x+4中，变量x每增加一个单位时，平均增加4个单位.
其中错误命题的序号是（ ）
A.①B.②C.③D.④
【答案】AB
【解析】
①线性相关系数r的绝对值越大，说明两个变量间线性相关性越强；
②给一组数据的每一个数同时加上或减去同一个常数，平均数会相应的增加或减小；
③方差反映一组数据的波动的大小，由方差公式可判断
④当x每增加一个单位时，可计算得
平均增加4个单位
解：①因为线性相关系数r的绝对值越大，说明两个变量间线性相关性越强，所以①不正确；
②给一组数据的每一个数同时加上或减去同一个常数，平均数会相应的增加或减小所加或减的常数，所以②不正确；
③方差反映一组数据的波动的大小，由方差公式知将一组数据中的每个数据都加上或减去同一个常数后，方差不变，所以③正确；
④当x每增加一个单位时，可计算得平均增加4个单位，所以④正确；
故选：AB
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图，在正三棱柱
中，
，
，由顶点
沿棱柱侧面经过棱
到顶点
的最短路线与棱的交点记为
，求：
（1）三棱柱的侧面展开科的对角线长；
（2）该最短路线的长及
的值；
（3）平面
与平面
所成二面角（锐角）的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列
的首项为
，前
项和为
，若对任意的
，均有
（
是常数且
）成立，则称数列
为“
数列”.
（1）若数列
为“
数列”，求数列
的通项公式；
（2）是否存在数列
既是“
数列”，也是“
数列”？若存在，求出符合条件的数列
的通项公式及对应的
的值；若不存在，请说明理由；
（3）若数列
为“
数列”， 
，设
，证明： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为F1(－c，0)，F2(c，0)，直线
交椭圆E于A，B两点，△ABF1的周长为16，△AF1F2的周长为12．
(1)求椭圆E的标准方程与离心率；
(2)若直线l与椭圆E交于C，D两点，且P(2，2)是线段CD的中点，求直线l的一般方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，函数
.
（1）当
时，解不等式
；
（2）若关于
的方程
的解集中恰有一个元素，求
的取值范围；
（3）设
，若对任意
，函数
在区间
上的最大值与最小值的差不超过1，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某海轮以每小时30海里的速度航行，在点
测得海面上油井
在南偏东
，海轮向北航行40分钟后到达点
，测得油井在南偏东
，海轮改为北偏东的航向再行驶80分钟到达点
，则
两点的距离为(单位：海里)
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
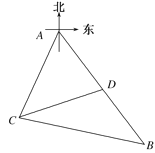
【题目】某观测站
在目标
的南偏西
方向，从
出发有一条南偏东
走向的公路，在
处测得与
相距
的公路
处有一个人正沿着此公路向
走去，走
到达
，此时测得
距离为
，若此人必须在
分钟内从
处到达
处，则此人的最小速度为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
过点
，离心率为
.
分别是椭圆
的上、下顶点，
是椭圆上异于的一点.
（1）求椭圆的方程；
（2）若点
在直线
上，且
，求
的面积；
（3）过点作斜率为
的直线分别交椭圆于另一点
，交
轴于点
，且点在线段
上（不包括端点
），直线
与直线
交于点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】绵阳是党中央、国务院批准建设的中国唯一的科技城，重要的国防科研和电子工业生产基地，市某科研单位在研发过程中发现了一种新合金材料，由大数据测得该产品的性能指标值
（值越大产品的性能越好）与这种新合金材料的含量
（单位：克）的关系为：当
时，是的二次函数；当
时，
测得部分数据如表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求关于的函数关系式
；
（2）求该新合金材料的含量为何值时产品的性能达到最佳．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
