
【题目】某市有两家共享单车公司,在市场上分别投放了黄、蓝两种颜色的单车,已知黄、蓝两种颜色的单车的投放比例为2:1.监管部门为了了解两种颜色的单车的质量,决定从市场中随机抽取5辆单车进行体验,若每辆单车被抽取的可能性相同.
(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率;
(2)在骑行体验过程中,发现蓝色单车存在一定质量问题,监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测,并规定若抽到的是蓝色单车,则抽样结束,若抽取的是黄色单车,则将其放回市场中,并继续从市场中随机地抽取下一辆单车,并规定抽样的次数最多不超过![]() (
(![]() )次.在抽样结束时,已取到的黄色单车以
)次.在抽样结束时,已取到的黄色单车以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(I) ![]() . (II) 见解析.
. (II) 见解析.
【解析】试题分析:(1) 设![]() 表示“抽取的5辆单车中蓝颜色单车的个数”,则
表示“抽取的5辆单车中蓝颜色单车的个数”,则![]() ~
~![]() ,可求5辆单车中有2辆是蓝颜色单车的概率.
,可求5辆单车中有2辆是蓝颜色单车的概率.
(2) ξ的可能取值为:0,1,2,…, ![]() . 并且有
. 并且有![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() . 可得ξ的分布列及
. 可得ξ的分布列及![]() 的数学期望,再由错位相减法求解即可.
的数学期望,再由错位相减法求解即可.
试题解析:(I) 因为随机地抽取一辆单车是蓝色单车的概率为![]() ,用
,用![]() 表示“抽取的5辆单车中蓝颜色单车的个数”,则
表示“抽取的5辆单车中蓝颜色单车的个数”,则![]() 服从二项分布,即
服从二项分布,即![]() ~
~![]() ,
,
所以抽取的5辆单车中有2辆是蓝颜色单车的概率![]() .
.
(2) ξ的可能取值为:0,1,2,…, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() .
.
所以ξ的分布列为:
ξ | 0 | 1 | 2 | …… |
|
|
|
|
|
| …… |
|
|
![]() 的数学期望为:
的数学期望为:
![]() , (1)
, (1)
![]() . (2)
. (2)
(1)-(2)得:
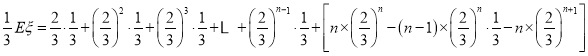
![]() ,
,
![]()
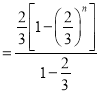
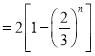 .
.
所以![]() .
.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且被
,且被![]() 轴所截得的弦长为
轴所截得的弦长为![]() ,圆心
,圆心![]() 在第一象限.
在第一象限.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,当△
,当△![]() 的面积最小时,求切线
的面积最小时,求切线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级参加期末考试的学生中抽出60名,其成绩(均为整数)的频率分布直方图如图所示,由此估计此次考试成绩的中位数、众数分别是( )
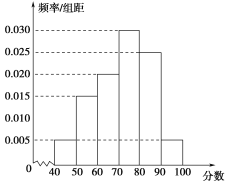
A.73.3,75B.73.3,80
C.70,70D.70, 75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com