
【题目】设函数![]()
(1)当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)若函数![]() 在[1,3]上存在单调递增区间,求实数
在[1,3]上存在单调递增区间,求实数![]() 的取值范围.
的取值范围.
【答案】![]() m=﹣2或m
m=﹣2或m![]() ln2;
ln2;![]() (﹣∞,
(﹣∞,![]() )
)
【解析】
(1)将a=0代入f(x),求出f(x)的导数,得到f′(x)=3,解得x的值,求出切点坐标,代入求出m的值即可;
(2)假设函数f(x)在[1,3]上不存在单调递增区间,必有g(x)≤0,得到关于a的不等式组,解出即可.
(1)当a=0时,f(x)=lnx+x2,x∈(0,+∞),
f′(x)![]() 2x>0,
2x>0,
令f′(x)=3,解得:x=1或x![]() ,
,
代入f(x)得切点坐标为(1,1),或(![]() ,
,![]() ln2),
ln2),
将切点坐标代入直线y=3x+m,解得:m=﹣2或m![]() ln2;
ln2;
(2)f′(x)![]() 2x﹣2a
2x﹣2a![]() ,x∈[1,3],
,x∈[1,3],
设g(x)=2x2﹣2ax+1,
假设函数f(x)在[1,3]上不存在单调递增区间,必有g(x)≤0,
于是 ,解得:a
,解得:a![]() ,
,
故要使函数f(x)在[1,3]上存在单调递增区间,
则a的范围是(﹣∞,![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,满足
,满足![]() 的实数
的实数![]() 有且只有
有且只有![]() 个,给出下述四个结论:
个,给出下述四个结论:
①满足题目条件的实数![]() 有且只有
有且只有![]() 个;②满足题目条件的实数
个;②满足题目条件的实数![]() 有且只有
有且只有![]() 个;
个;
③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() .
.
其中所有正确结论的编号是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 经统计,试销这10天两个商家每天的销量如图所示的茎叶图(茎为十位数字,叶为个位数字):
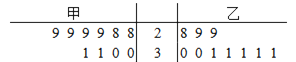
(1)现从甲商家试销的10天中随机抽取两天,求这两天的销售量都小于30件的概率;
(2)根据试销10天的数据,将频率视作概率,用样本估计总体,回答以下问题:
①记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
②超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日返利额的数学期望考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 命题“,使得
命题“,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
④命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
其中所有正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.

(Ⅰ)证明:AB1⊥平面A1B1C1;
(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com