
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为非零常数.
为非零常数.
(1)若![]() ,
, ![]() ,求证:
,求证: ![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公差不等于零的等差数列.
是公差不等于零的等差数列.
①求实数![]() ,
, ![]() 的值;
的值;
②数列![]() 的前
的前![]() 项和
项和![]() 构成数列
构成数列![]() ,从
,从![]() 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为![]() 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
【答案】(1)![]() (2)①
(2)①![]() ,
, ![]() ,
, ![]() .②
.②![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)利用等比数列定义证明,即寻找![]() 与
与![]() 比例关系:利用
比例关系:利用![]() 代入化简可得
代入化简可得![]() .最后说明各项非零.(2)①令
.最后说明各项非零.(2)①令![]() ,2,3,根据等差数列性质得
,2,3,根据等差数列性质得![]() ,列出关于
,列出关于![]() ,
, ![]() 的二元一次方程组,解得
的二元一次方程组,解得![]() ,
, ![]() 的值;再验证满足题意. ②先求数列
的值;再验证满足题意. ②先求数列![]() 的前
的前![]() 项和
项和![]() ,再讨论四项奇偶性:三个奇数一个偶数、或者一个奇数三个偶数.将奇偶性代入化简讨论,直至确定.
,再讨论四项奇偶性:三个奇数一个偶数、或者一个奇数三个偶数.将奇偶性代入化简讨论,直至确定.
试题解析:解:(1)当![]() ,
, ![]() 时,
时, ![]()
![]()
![]() ,
,
![]() .
.
又![]() ,不然
,不然![]() ,这与
,这与![]() 矛盾,
矛盾,
![]() 为2为首项,3为公比的等比数列,
为2为首项,3为公比的等比数列,
![]() ,
, ![]() .
.
(2)①设![]()
![]() ,
,
由![]() 得
得![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
对任意![]() 恒成立.
恒成立.
令![]() ,2,3,解得,
,2,3,解得, ![]() ,
, ![]() ,
, ![]() .
.
经检验,满足题意.
综上, ![]() ,
, ![]() ,
, ![]() .
.
②由①知![]() .
.
设存在这样满足条件的四元子列,观察到2017为奇数,这四项或者三个奇数一个偶数、或者一个奇数三个偶数.
1°若三个奇数一个偶数,设![]() ,
, ![]() ,
, ![]() ,
, ![]() 是满足条件的四项,
是满足条件的四项,
则![]()
![]() ,
,
![]()
![]() ,这与1007为奇数矛盾,不合题意舍去.
,这与1007为奇数矛盾,不合题意舍去.
2°若一个奇数三个偶数,设![]() ,
, ![]() ,
, ![]() ,
, ![]() 是满足条件的四项,
是满足条件的四项,
则![]()
![]() ,
, ![]() .
.
由504为偶数知, ![]() ,
, ![]() ,
, ![]() 中一个偶数两个奇数或者三个偶数.
中一个偶数两个奇数或者三个偶数.
1)若![]() ,
, ![]() ,
, ![]() 中一个偶数两个奇数,不妨设
中一个偶数两个奇数,不妨设![]() ,
, ![]() ,
, ![]() ,
,
则![]()
![]() ,这与251为奇数矛盾.
,这与251为奇数矛盾.
2)若![]() ,
, ![]() ,
, ![]() 均为偶数,不妨设
均为偶数,不妨设![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,继续奇偶分析知
,继续奇偶分析知![]() ,
, ![]() ,
, ![]() 中两奇数一个偶数,
中两奇数一个偶数,
不妨设![]() ,
, ![]() ,
, ![]() ,则
,则![]()
![]() .
.
因为![]() ,
, ![]() 均为偶数,所以
均为偶数,所以![]() 为奇数,不妨设
为奇数,不妨设![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
即![]() ,
, ![]() ,
, ![]() ,
, ![]() 或者
或者![]() ,
, ![]() ,
, ![]() ,
, ![]() 或者
或者![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足条件,
满足条件,
综上所述, ![]() ,
, ![]() ,
, ![]() 为全部满足条件的四元子列.
为全部满足条件的四元子列.


科目:高中数学 来源: 题型:
【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3 ![]() km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= ![]() ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
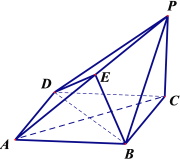
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)当![]() ,
, ![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同实数解,求
上有两个不同实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
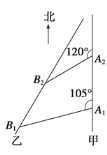
【题目】如图所示,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10![]() 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园![]() ,公园由长方形的休闲区
,公园由长方形的休闲区![]() (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区![]() 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长![]() 米,求公园
米,求公园![]() 所占面积
所占面积![]() 关于
关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区![]() 的长和宽该如何设计?
的长和宽该如何设计?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
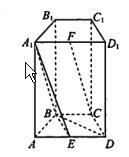
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com