
【题目】已知cos(75°+α)=![]() ,α是第三象限角,
,α是第三象限角,
(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
【答案】(1)-![]() ;(2)-
;(2)-![]() ; (3)
; (3)![]() .
.
【解析】
试题分析:
(1)由题意可得![]() 是第四象限角,结合同角三角函数基本关系可得
是第四象限角,结合同角三角函数基本关系可得![]() ;
;
(2)利用诱导公式和(1)的结论可得cos(α-15°) 的值为![]()
(3)由题意结合诱导公式可得:sin(195°-α) +cos(105o-α)=-sin[90°-(75°+α)] -cos(75°+α)![]() .
.
试题解析:
(1)∵cos(75°+α)=![]() >0,α是第三象限角,
>0,α是第三象限角,
∴75°+α是第四象限角,
且sin(75°+α)=![]()
(2)cos(α-15°)= cos[90°-(75°+α)]= sin(75°+α)= -![]()
(3)sin(195°-α) +cos(105o-α)
=sin[180°+(15°-α)]+cos[180o o-(75°+α)]
=-sin(15°-α) -cos(75°+α)
=-sin[90°-(75°+α)] -cos(75°+α)
=-2cos(75°+α)=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(题文)“你低碳了吗?”这是某市为倡导建设节约型社会而发布的公益广告里的一句话,活动组织者为了了解这则广告的宣传效果,随机抽取了120名年龄在![]() ,
,![]() ,…,
,…,![]() 的市民进行问卷调查,由此得到的样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到的样本的频率分布直方图如图所示.
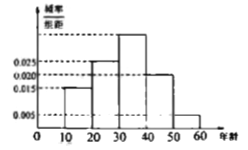
(1)根据直方图填写频率分布统计表;
(2)根据直方图,试估计受访市民年龄的中位数(保留整数);
(3)如果按分层抽样的方法,在受访市民样本年龄在![]() 中共抽取5名市民,再从这5人中随机选2人作为本次活动的获奖者,求年龄在
中共抽取5名市民,再从这5人中随机选2人作为本次活动的获奖者,求年龄在![]() 和
和![]() 的受访市民恰好各有一人获奖的概率.
的受访市民恰好各有一人获奖的概率.
分组 | 频数 | 频率 |
| 18 | 0.15 |
| 30 | |
| ||
| 0.2 | |
| 6 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:
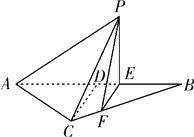
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() >0,
>0, ![]() ≠1,
≠1, ![]() ≠﹣1),是定义在(﹣1,1)上的奇函数.
≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求实数![]() 的值;
的值;
(2)当![]() =1时,判断函数
=1时,判断函数![]() 在(﹣1,1)上的单调性,并给出证明;
在(﹣1,1)上的单调性,并给出证明;
(3)若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的中心为点
的中心为点![]() ,
, ![]() 边所在的直线方程为
边所在的直线方程为![]() .
.
(1)求![]() 边所在的直线方程和正方形
边所在的直线方程和正方形![]() 外接圆的方程;
外接圆的方程;
(2)若动圆![]() 过点
过点![]() ,且与正方形
,且与正方形![]() 外接圆外切,求动圆圆心
外接圆外切,求动圆圆心![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车是碳排放量比较大的交通工具,某地规定,从2017年开始,将对二氧化碳排放量超过130 g/km的轻型汽车进行惩罚性征税,检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() =120 g/km.
=120 g/km.
(1)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130 g/km的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}满足 ![]() =pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
=pn+r(p,r为常数),其中Sn为数列{an}的前n项和.
(1)若p=1,r=0,求证:{an}是等差数列;
(2)若p= ![]() ,a1=2,求数列{an}的通项公式;
,a1=2,求数列{an}的通项公式;
(3)若a2015=2015a1 , 求pr的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com