已知f(x)=loga(x+1),点P是函数y=f(x)图象上的任意一点,点P关于原点的对称点Q形成函数y=g(x)的图象.
(1)求y=g(x)的解析式;
(2)当0<a<1时,解不等式2f(x)+g(x)≥0;
(3)当a>1,且x∈[0,1)时,总有2f(x)+g(x)≥m恒成立,求m的取值范围.
【答案】
分析:(1)由已知条件可知函数g(x)的图象上的任意一点Q(x,y)关于原点对称的点P(-x,-y)在函数f(x)图象上,把P(-x,-y)代入f(x),整理可得g(x)
(2)由2f(x)+g(x)≥0得2log
a(x+1)≥log
a(1-x)去掉对数符号后转化为整式不等式,从而求得x的取值范围;
(3)由(1)可令h(x)=2f(x)+g(x),
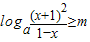
,令
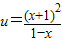
,先判断函数u(x)在(0,1]的单调性,进而求得函数的最小值h(x)
min,使得m≤h(x)
min解答:解:(1)设Q(x,y),
∵P、Q两点关于原点对称,
∴P点的坐标为(-x,-y),又点p(-x,-y)在函数y=f(x)的图象上,
∴-y=log
a(-x+1),即g(x)=-log
a(1-x)…(2分)
(2)由2f(x)+g(x)≥0得2log
a(x+1)≥log
a(1-x)
∵0<a<1∴
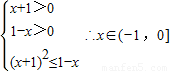
…(6分)
(3)由题意知:a>1且x∈[0,1)时
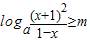
恒成立.…(7分)
设
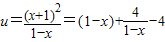
,令t=1-x,t∈(0,1],
∴
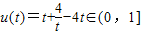
…(9分)
设0<t
1<t
2≤1∵

∴u(t)在t∈(0,1]上单调递减,
∴u(t)的最小值为1…(12分)
又∵a>1,∴
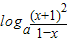
的最小值为0…(13分)
∴m的取值范围是m≤0…(14分)
点评:本题(1)小题主要考查了函数的中心对称问题:若函数y=f(x)与y=g(x)关于点M(a,b)对称,则y=f(x)上的任意一点(x,y)关于M(a,b)对称的点(2a-x,2b-y)在函数y=g(x)的图象上.(3)小题主要考查了函数的恒成立问题,往往转化为求最值问题:m≥h(x)恒成立,则m≥h(x)
max,m≤h(x)恒成立,则m≤h(x)
min

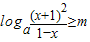 ,令
,令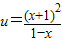 ,先判断函数u(x)在(0,1]的单调性,进而求得函数的最小值h(x)min,使得m≤h(x)min
,先判断函数u(x)在(0,1]的单调性,进而求得函数的最小值h(x)min,使得m≤h(x)min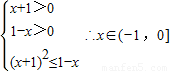 …(6分)
…(6分)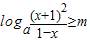 恒成立.…(7分)
恒成立.…(7分)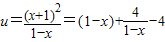 ,令t=1-x,t∈(0,1],
,令t=1-x,t∈(0,1],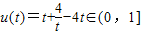

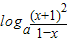 的最小值为0…(13分)
的最小值为0…(13分)

 阅读快车系列答案
阅读快车系列答案