
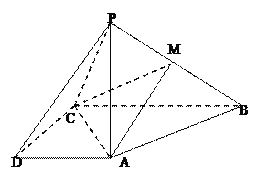
【题目】如图,在四棱锥![]() 中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.
中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中点.
(1)求证:AM||平面PCD;
(2)求证:平面ACM⊥平面PAB;
(3)若PC与平面ACM所成角为30°,求PA的长.
【答案】(1)见解析.
(2)见解析.
(3) ![]() .
.
【解析】分析:(1)利用向量法证明![]() 即得AM||平面PCD.(2)利用向量法证明
即得AM||平面PCD.(2)利用向量法证明![]() ,即得平面ACM⊥平面PAB.(3)利用向量法解答,根据PC与平面ACM所成角为30°得到关于关于a的方程,解方程得到a的值,再求PA的长.
,即得平面ACM⊥平面PAB.(3)利用向量法解答,根据PC与平面ACM所成角为30°得到关于关于a的方程,解方程得到a的值,再求PA的长.
详解:(1)如图以C为原点建立空间直角坐标系C-xyz,
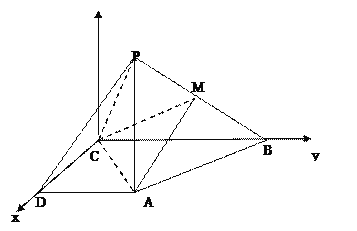
A(1,1,0),B(0,2,0),C(0,0,0),D(1,0,0),P(1,1,a)(a>0)
M(![]() ),
),![]() =(1,1,a),
=(1,1,a),![]() =(1,0,0)
=(1,0,0)
设平面PCD法向量为![]() ,
,
令![]() ,则
,则![]() =(0,a,-1),
=(0,a,-1),
所以![]() ,
,![]()
所以AM||平面PCD
(2)![]() =(1,1,0),
=(1,1,0),![]() ,设平面ACM法向量为
,设平面ACM法向量为![]() ,
,
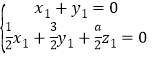 令
令![]() ,则
,则![]() ,
,
![]() (0,0,a),
(0,0,a),![]() =(-1,1,0)设平面PAB法向量为
=(-1,1,0)设平面PAB法向量为![]() ,
,
![]() 令
令![]() ,则
,则![]() =(1,1,0),
=(1,1,0),
所以![]() .
.
所以平面ACM⊥平面PAB .
(3)由题得![]() =(1,1,a),
=(1,1,a),
所以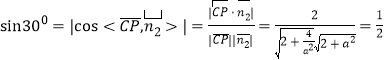
解得![]() ,所以PA的长为
,所以PA的长为![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
![]() .
.
(1)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(2)在(1)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标平面内,每个点绕原点按逆时针方向旋转![]() 的变换
的变换![]() 所对应的矩阵为
所对应的矩阵为![]() ,每个点横、纵坐标分别变为原来的
,每个点横、纵坐标分别变为原来的![]() 倍的变换
倍的变换![]() 所对应的矩阵为
所对应的矩阵为![]() .
.
(I)求矩阵![]() 的逆矩阵
的逆矩阵![]() ;
;
(Ⅱ)求曲线![]() 先在变换
先在变换![]() 作用下,然后在变换
作用下,然后在变换![]() 作用下得到的曲线方程.
作用下得到的曲线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市气象站观测点记录的连续![]() 天里,
天里,![]() 指数(空气质量指数)
指数(空气质量指数)![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位cm)的情况如下表1:
(单位cm)的情况如下表1:
表1
|
|
|
|
|
|
|
|
|
|
该市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
表2
|
|
|
|
|
|
频数 |
|
|
|
|
|
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式:![]() ;其中
;其中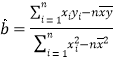 ,
,![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于
不高于![]() 时,洗车店平均每天亏损约
时,洗车店平均每天亏损约![]() 元;当
元;当![]() 在
在![]() 至
至![]() 时,洗车店平均每天收入月
时,洗车店平均每天收入月![]() 元;当
元;当![]() 大于
大于![]() 时,洗车店平均每天收入约
时,洗车店平均每天收入约![]() 元;根据表
元;根据表![]() 估计小张的洗车店该月份平均每天的收入.
估计小张的洗车店该月份平均每天的收入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com