
【题目】给出下列命题:
①![]() ,不等式
,不等式![]() 恒成立;
恒成立;
②若![]() ,则
,则![]() ;
;
③“若![]() 且
且![]() ,则
,则![]() ”的逆否命题;
”的逆否命题;
④若命题![]() ,命题
,命题![]() ,则命题
,则命题![]() 是真命题.
是真命题.
其中,真命题为( )
A.①③④B.①②C.①②③D.②③④
【答案】C
【解析】
对于①中不等式可表示为![]() 得结论;对于②根据基本不等式的适用条件,结合
得结论;对于②根据基本不等式的适用条件,结合![]() 与
与![]() 互为倒数,是同号的两个数,可得
互为倒数,是同号的两个数,可得![]() ,可得结论;对于③根据逆否命题与原命题同真同假,直接判断原命题的真假即可,然后利用不等式的基本性质,可以证出原命题为真命题;对于④可以分别证出命题
,可得结论;对于③根据逆否命题与原命题同真同假,直接判断原命题的真假即可,然后利用不等式的基本性质,可以证出原命题为真命题;对于④可以分别证出命题![]() 和命题
和命题![]() 都是真命题,从而得到题
都是真命题,从而得到题![]() 是假命题.
是假命题.
对于①,不等式![]() 整理,得原不等式等价于
整理,得原不等式等价于![]() ,
,
∵![]()
∴原不等式恒成立,故①正确;
对于②,因为![]() ,两个数互为倒数,
,两个数互为倒数,
所以![]() 与
与![]() 同号,当
同号,当![]() 时,
时,
可得![]() 与
与![]() 都为正数,
都为正数,
根据基本不等式,有![]() ,
,
此时有![]() 且
且![]() ,
,
∴![]() ,故②正确;
,故②正确;
对于③,命题“若![]() 且
且![]() ,则
,则![]() ”的逆否命题与原命题同真同假,
”的逆否命题与原命题同真同假,
因此判断原命题的真假性即可,
若![]() ,两边都除以
,两边都除以![]() ,得
,得![]() …(),
…(),
又因为![]() ,将()两边都乘以
,将()两边都乘以![]() ,得
,得![]() ,
,
所以原命题是真命题,故③是真命题,正确;
对于④,∵![]() 对任意的
对任意的![]() 均成立,
均成立,
∴命题![]() ”是真命题,
”是真命题,
∵存在![]() ,使得
,使得![]() ,
,
∴命题![]() 是真命题,
是真命题,
∴命题![]() 是假命题,
是假命题,
∵命题“![]() ”当中有一个真命题,另一个是假命题
”当中有一个真命题,另一个是假命题
∴“![]() ”是假命题,故④不正确,
”是假命题,故④不正确,
综上所述,真命题有三个:①②③,
故选:C.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 定义域为
定义域为![]() ,且对任意实数
,且对任意实数![]() ,有
,有![]() ,则称
,则称![]() 为“
为“![]() 形函数”,若函数
形函数”,若函数![]() 定义域为
定义域为![]() ,函数
,函数![]() 对任意
对任意![]() 恒成立,且对任意实数
恒成立,且对任意实数![]() ,有
,有![]() ,则称为“对数
,则称为“对数![]() 形函数” .
形函数” .
(1)试判断函数![]() 是否为“
是否为“![]() 形函数”,并说明理由;
形函数”,并说明理由;
(2)若![]() 是“对数
是“对数![]() 形函数”,求实数
形函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 是“
是“![]() 形函数”,且满足对任意
形函数”,且满足对任意![]() ,有
,有![]() ,问
,问![]() 是否为“对数
是否为“对数![]() 形函数”?证明你的结论.
形函数”?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节过后,某市教育局从全市高中生中抽去了100人,调查了他们的压岁钱收入情况,按照金额(单位:百元)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示:
.统计结果如下表所示:
![]()
该市高中生压岁钱收入![]() 可以认为服从正态分布
可以认为服从正态分布![]() ,用样本平均数
,用样本平均数![]() (每组数据取区间的中点值)作为
(每组数据取区间的中点值)作为![]() 的估计值.
的估计值.
(1)求样本平均数![]() ;
;
(2)求![]() ;
;
(3)某文化公司赞助了市教育局的这次社会调查活动,并针对该市的高中生制定了赠送“读书卡”的活动,赠送方式为:压岁钱低于![]() 的获赠两次读书卡,压岁钱不低于
的获赠两次读书卡,压岁钱不低于![]() 的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:
的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:

现从该市高中生中随机抽取一人,记![]() (单位:张)为该名高中生获赠的读书卡的张数,求
(单位:张)为该名高中生获赠的读书卡的张数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以原点
).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与圆
与圆![]() 有公共点,试求实数
有公共点,试求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,过点
时,过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国有一道古典数学名著——两鼠穿墙:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”题意是:“有两只老鼠从墙的两边打洞穿墙(连线与墙面垂直),大老鼠第一天进一尺,以后每天加倍,小老鼠第一天也进一尺,以后每天减半,那么两鼠第几天能见面.”假设墙厚16尺,如图是源于该题思想的一个程序框图,则输出的![]() ( )
( )
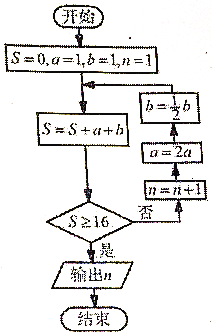
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,圆心为
,圆心为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线
在直线![]() 上,过
上,过![]() 点作圆
点作圆![]() 的切线
的切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.
(1)若![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:经过![]() ,
,![]() ,
,![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从数列![]() 中取出部分项组成的数列称为数列
中取出部分项组成的数列称为数列![]() 的“子数列”.
的“子数列”.
(1)若等差数列![]() 的公差
的公差![]() ,其子数列
,其子数列![]() 恰为等比数列,其中
恰为等比数列,其中![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否为
是否为![]() 的“子数列”,并证明你的结论.
的“子数列”,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com