Question

已知直线与曲线恰有两个不同的交点，记k的所有可能取值构成集合A；P(x，y)是椭圆上一动点，与点P关于直线y＝x＋1对称，记的所有可能取值构成集合B，若随机的从集合A，B中分别抽出一个元素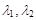，则的概率是___________

Answer 1

解析试题分析：由，当x≥0时，显然k＞0，两边平方得
，即
由题意，该方程有两个不相等的正实数根
即即结合k＞0解得k∈(0，1)，即A＝(0，1)
对于椭圆，由于原点关于y＝x＋1的对称点为(－1，1)
所以，椭圆关于y＝x＋1的对称椭圆为，
在改椭圆上，可知y₁－1∈[－4，4]
于是∈[－1，1]，即B＝[－1，1]
【方法一】由，分别以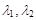为横坐标和纵坐标，
可知点(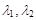)构成一个面积为2的矩形
其中满足的是图中阴影部分，面积为
所以，满足的概率是

【方法二】当时，此事件发生的概率为，此时必有
当时，此事件发生的概率为，此时与概率相等，各占，于是此时满足的概率为.
以上两事件互斥，且[－1，0]与(0，1]的区间长度相等，故满足的概率为.
考点：直线与曲线的交点，轴对称图形，坐标的取值范围，几何概型.