
【题目】已知![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,
, ![]() ,
, ![]() 为函数
为函数![]() 的两个零点,求证:
的两个零点,求证: ![]() .
.
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】试题分析: (Ⅰ)根据导数![]() ,分类讨论,当
,分类讨论,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, 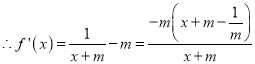 ,由
,由![]()
得![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,即可得出单调区间;(Ⅱ)由(Ⅰ)知
,即可得出单调区间;(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .不妨设
.不妨设![]() ,由条件知
,由条件知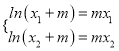 ,即
,即![]() ,构造函数
,构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]() ,利用单调性只需证
,利用单调性只需证![]()
构造函数利用单调性证明.
试题解析:(Ⅰ) ![]() ,
, ![]()
当![]() 时,
时, ![]() ,即
,即![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,
时, 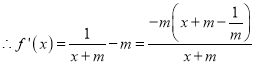 ,由
,由![]()
得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
![]() 时,易知
时,易知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
不妨设![]() ,由条件知
,由条件知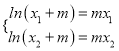 ,即
,即![]()
构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]()
由![]() 可得
可得![]() ,
,
而![]() ,
, ![]()
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
可知![]()
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]()
考虑到![]() 在
在![]() 上递增,只需证
上递增,只需证![]()
由![]() 知,只需证
知,只需证![]()
令![]() ,
,
则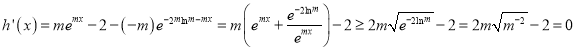
即![]() 单增,又
单增,又![]() ,
,
结合![]() 知
知![]() ,即
,即![]() 成立,
成立,
即![]() 成立
成立


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1,C2的极坐标方程分别为ρ=2cosθ, ![]() ,射线θ=φ,
,射线θ=φ, ![]() ,
, ![]() 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)当![]() 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合M满足M{1,2,3},且M中至少有一个奇数,这样的集合M有6个;
②已知函数f(x)= ![]() 的定义域是R,则实数a的取值范围是(﹣12,0);
的定义域是R,则实数a的取值范围是(﹣12,0);
③函数f(x)=loga(x﹣3)+1(a>0且a≠1)图象恒过定点(4,2);
④已知函数f(x)=x2+bx+c对任意实数t都有f(3+t)=f(3﹣t),则f(1)>f(4)>f(3).
其中正确的命题序号是(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

(1)令![]() ,利用给出的参考数据求出
,利用给出的参考数据求出![]() 关于
关于![]() 的回归方程
的回归方程![]() .(
.(![]() ,
,![]() 精确到0.1)
精确到0.1)
参考数据:![]() ,
,![]() ,
,![]()
其中![]() ,
,![]()
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com