
【题目】如图,在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1 , AC与BD的交点为O.
(1)求证:直线OO1∥平面BCC1B1;
(2)若AB=BC,求证:直线BO⊥平面ACC1A1 .
【答案】
(1)证明:在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1,O1是A1C1的中点.
AC与BD的交点为O.O是AC的中点.
ACC1A1是矩形,可知OO1∥CC1,CC1平面BCC1B1,
OO1平面BCC1B1,
∴直线OO1∥平面BCC1B1

(2)证明:AB=BC,所以△ABC是等腰三角形,BO⊥AC,AA1⊥BO,AA1∩AC=A,
∴直线BO⊥平面ACC1A1.
【解析】第(1)问应用线面平行的判定定理即可。
第(2)问要正面线面垂直,关键是线垂直于面内两条线,因此只要证明BO⊥AC,AA1⊥BO即可;
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中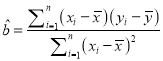
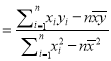 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过三点A(﹣3,2),B(3,﹣6),C(0,3)的圆的方程为( )
A.x2+y2+4y﹣21=0
B.x2+y2﹣4y﹣21=0
C.x2+y2+4y﹣96=0
D.x2+y2﹣4y﹣96=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】联合国教科文组织规定,每年的4月23日是“世界读书日”.某校研究生学习小组为了解本校学生的阅读情况,随机调查了本校400名学生在这一天的阅读时间![]() (单位:分钟),将时间数据分成5组:
(单位:分钟),将时间数据分成5组:![]() ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
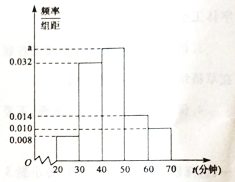
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这400名学生中抽取50人参加交流会,则在阅读时间为![]() 的两组中分别抽取多少人?
的两组中分别抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,家庭的月理财投入![]() (单位:千元)与月收入
(单位:千元)与月收入![]() (单位:千元)之间具有线性相关关系.某银行随机抽取5个家庭,获得第
(单位:千元)之间具有线性相关关系.某银行随机抽取5个家庭,获得第![]() (
(![]() 1,2,3,4,5)个家庭的月理财投入
1,2,3,4,5)个家庭的月理财投入![]() 与月收入
与月收入![]() 的数据资料,经计算得
的数据资料,经计算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若某家庭月理财投入为5千元,预测该家庭的月收入.
附:回归方程的斜率与截距的最小二乘估计公式分别为:
 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥![]() 面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:![]() ;
;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(3)当二面角![]() 的大小为
的大小为![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
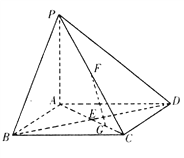
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() .
.
(1)求![]() 的值并求函数
的值并求函数![]() 的值域;
的值域;
(2)若关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为
的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com