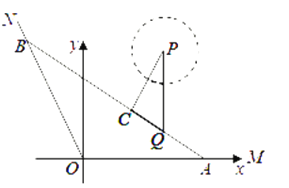
【题目】如图，A、B是海岸线OM、ON上两个码头，海中小岛有码头Q到海岸线OM、ON的距离分别为
、
，测得
，
，以点O为坐标原点，射线OM为x轴的正半轴，建立如图所示的直角坐标系，一艘游轮以
小时的平均速度在水上旅游线AB航行（将航线AB看作直线，码头Q在第一象限，航线BB经过点Q）.
（1）问游轮自码头A沿
方向开往码头B共需多少分钟？
（2）海中有一处景点P（设点P在
平面内，
，且
），游轮无法靠近，求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】狄利克雷函数为F(x)
.有下列四个命题：①此函数为偶函数，且有无数条对称轴；②此函数的值域是
；③此函数为周期函数，但没有最小正周期；④存在三点
，使得△ABC是等腰直角三角形，以上命题正确的是（ ）
A.①②B.①③C.③④D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
在区间
上有最大值4，最小值1，设函数
．
（1）求
、
的值及函数
的解析式；
（2）若不等式
在
时恒成立，求实数
的取值范围；
（3）如果关于
的方程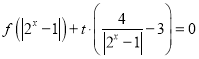
有三个相异的实数根，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司要在一条笔直的道路边安装路灯，要求灯柱AB与底面垂直，灯杆BC与灯柱AB所在的平面与道路走向垂直，路灯C采用锥形灯罩，射出的管线与平面ABC部分截面如图中阴影所示，
路宽AD=24米，设
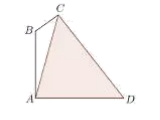
（1）求灯柱AB的高h（用
表示）；
（2）此公司应该如何设置的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小？最小值为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的奇数项是首项为1的等差数列，偶数项是首项为2的等比数列.设数列的前n项和为
且满足
（1）求数列的通项公式；
（2）若
求正整数
的值；
（3）是否存在正整数，使得
恰好为数列的一项？若存在，求出所有满足条件的正整数；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
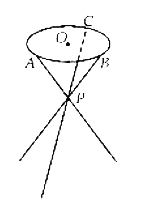
【题目】如图，小凳凳面为圆形，凳脚为三根细钢管.考虑到钢管的受力等因素，设计的小凳应满足：三根细钢管相交处的节点
与凳面圆形的圆心
的连线垂直于凳面和地面，且分细钢管上下两段的比值为
，三只凳脚与地面所成的角均为
.若
、
、
是凳面圆周的三等分点，
厘米，求凳子的高度
及三根细钢管的总长度(精确到
).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
是双曲线
的一条渐近线，点
在双曲线C上，设坐标原点为O.
（1）求双曲线C的方程；
（2）若过点
的直线l与双曲线C交于R、S两点，若
，求直线l的方程；
（3）设
在双曲线上，且直线AM与y轴相交于点P，点M关于y轴对称的点为N，直线AN与y轴相交于点Q，问：在x轴上是否存在定点T，使得
？若存在，求出点T的坐标；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为
的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆.
（1）若围墙AP,AQ总长度为200米，如何围可使得三角形地块APQ的面积最大？
（2）已知AP段围墙高1米，AQ段围墙高1.5米，造价均为每平方米100元.若围围墙用了20000元，问如何围可使竹篱笆用料最省？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，已知曲线
的方程为
，曲线
的方程为
．以极点
为原点，极轴为
轴正半轴建立直角坐标系
．
（1）求曲线，的直角坐标方程；
（2）若曲线与
轴相交于点
，与曲线相交于
，
两点，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
