
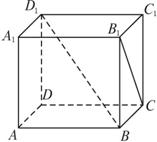
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.
(1)证明:∵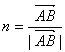 ,所以
,所以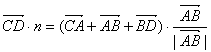 .由于CA⊥AB,BD⊥AB,∴
.由于CA⊥AB,BD⊥AB,∴![]() ,
,![]() .因此
.因此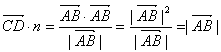 .?
.?
(2)解:先找一个向量n,它既与BD1垂直,又与B1C垂直.设![]() ,其中λ、μ为待定的数.
,其中λ、μ为待定的数.

由![]() =-a2-λa2+μa2=-a2(1+λ-μ)=0,∴1+λ-μ=0.
=-a2-λa2+μa2=-a2(1+λ-μ)=0,∴1+λ-μ=0.
又由![]()
=-a2-μa2=0,∴1+μ=0.
于是解得μ=-1,λ=-2,∴![]() ,
,
![]() .
.
又BC是联结这两条异面直线BD1与B1C上的任意点的线段,由第(1)题知所求距离为
![]() .
.
启示:(1)在以上推导中,我们已暗中假定了n的方向是由l1上的点A指向l2上的点B,而![]() 的方向也是由l1上的点C指向l2上的点D,这样求得
的方向也是由l1上的点C指向l2上的点D,这样求得![]() 是正值.如果n指向与
是正值.如果n指向与![]() 指向不同,则
指向不同,则![]() 是负值,所以一般地就写成
是负值,所以一般地就写成![]() .又如果n不是单位向量,则
.又如果n不是单位向量,则![]() .
.
(2)![]() 、
、![]() 、
、![]() 有着基底的作用,我们将BD1与B1C的公垂线段向量n用这组基底来表示.因为相差一个常数因子不影响其公垂性,所以设定了
有着基底的作用,我们将BD1与B1C的公垂线段向量n用这组基底来表示.因为相差一个常数因子不影响其公垂性,所以设定了![]() ,使其只含有两个待定常数,这样就方便多了.
,使其只含有两个待定常数,这样就方便多了.


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.?
查看答案和解析>>
科目:高中数学 来源: 题型:
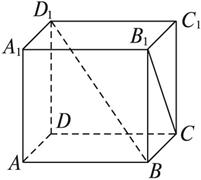
(2)已知正方体ABCD—A1B1C1D1的棱长为a,求体对角线BD1与面对角线B1C的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com