
【题目】已知函数 ![]() .
.
(1)求函数 ![]() 的单调区间和极值;
的单调区间和极值;
(2)是否存在实数 ![]() ,使得函数
,使得函数 ![]() 在
在 ![]() 上的最小值为
上的最小值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)解:由题意知, ![]() .
.
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函数
,所以函数 ![]() 的单调增区间是
的单调增区间是 ![]() ;
;
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函数
,所以函数 ![]() 的单调减区间是
的单调减区间是 ![]() .
. ![]() 当
当 ![]() 时,函数
时,函数 ![]() 有极小值为
有极小值为 ![]()
(2)解:由(1)可知,当 ![]() 时,
时, ![]() 单调递减,当
单调递减,当 ![]() 时,
时, ![]() 单调递增.
单调递增.
①若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上为增函数,故函数
上为增函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,显然
,显然 ![]() ,故不满足条件.
,故不满足条件.
②若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上为减函数,在
上为减函数,在 ![]() 上为增函数,故函数
上为增函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,而
,而 ![]() ,故不满足条件.
,故不满足条件.
③若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在在
在在 ![]() 上为减函数,故函数
上为减函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,即
,即 ![]() ,而
,而 ![]() 不满足条件,综上所述,这样的
不满足条件,综上所述,这样的 ![]() 不存在
不存在
【解析】(1)根据题意求出原函数的导函数再利用导函数的正负得出原函数的增减性。(2)首先求出原函数的导函数由导函数大于零解出x的取值范围然后对a分三种情况讨论,再利用f ( x ) 在 [ 1 , e ] 上的最小值为 0求出a的值即可。
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)当![]() 时,写出
时,写出![]() 的通项公式(直接写出答案,无需过程);
的通项公式(直接写出答案,无需过程);
(2)求最小整数![]() ,使得当
,使得当![]() 时,
时, ![]() 是单调递增数列;
是单调递增数列;
(3)是否存在![]() 使得
使得![]() 是等比数列?若存在请求出;若不存在请说明理由.
是等比数列?若存在请求出;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2 ![]() sin
sin ![]() ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据,
(吨标准煤)的几组对照数据,

(1)求![]() ,
, ![]() ,
,
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技动前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
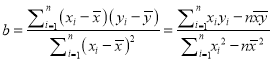 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出一个著名的猜想:任给一个正整数 ![]() ,如果
,如果 ![]() 是偶数,就将它减半(即
是偶数,就将它减半(即 ![]() );如果
);如果 ![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即 ![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数 ![]() (首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则
(首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则 ![]() 的所有不同值的个数为 .
的所有不同值的个数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com