
����Ŀ����2007ȫ�˻�����������˶�Ա�ס����ڱ����д�����³ɼ���
�ף�9.4��8.7��7.5��8.4��10.1��10.5��10.7��7.2��7.8��10.8��
�ң�9.1��8.7��7.1��9.8��9.7��8.5��10.1��9.2��10.1��9.1��
��1���þ�Ҷͼ��ʾ�ף��������ɼ��������ݾ�Ҷͼ�����ס������˳ɼ���
��2���ֱ��������������ƽ����![]() �ͱ���
�ͱ���![]() �������ݼ�����������λ�˶�Ա�ijɼ��Ƚ��ȶ���
�������ݼ�����������λ�˶�Ա�ijɼ��Ƚ��ȶ���
���𰸡���1������������2��������
�������������������1������֪�е����ݣ����ǿɽ����������ֱ�ʾ����С�����ֱ�ʾҶ�����Ƴ�����ľ�Ҷͼ�������ݾ�Ҷͼ�����ݵ���״�����������������˶�Ա�ijɼ��ȶ��ԣ�
��2��������֪����������˶�Ա�ס����ڱ����д���ijɼ����������ݵ�ƽ������ʽ�����ʽ���Ƚ��������ݵķ�����ݱ귽��С���˶�Ա�ijɼ��Ƚ��ȶ������ɵõ��𰸣�
���������
��1����ͼ��ʾ������ʾ�ɼ�������������Ҷ��ʾС���������֡�
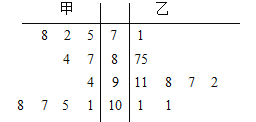
����ͼ֪������λ����9.05������λ����9.15���ҵijɼ����¶Գƣ�
���Կ����ҷ����ȶ��Ժã��ײ����Դ�
��2���⣺��3��![]() ����
����![]() ����9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8��=9.11
����9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8��=9.11
S����![]() ��1.3
��1.3
![]() ����
����![]() ����9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1����9.14
����9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1����9.14
S����![]() ��0.9
��0.9
��S��>S������˵���˼��˶�Ա�IJ����������˶�Ա�IJ������������ǹ��ƣ����˶�Ա�Ƚ��ȶ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC��������ABCD�л��ഹֱ���⣬BC=2����AD=2c����AB+BD=AC+CD=2a������a��cΪ��������������ABCD����������ֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶������߶��Լ��IJ����˶�����![]() ����λ��ǧ�ף��Ͳ����˶�ʱ��
����λ��ǧ�ף��Ͳ����˶�ʱ��![]() ����λ�����ӣ�����ͳ�ƣ��õ����µ�ͳ�����ϣ�
����λ�����ӣ�����ͳ�ƣ��õ����µ�ͳ�����ϣ�

���![]() ��
��![]() ����������ع�ϵ��
����������ع�ϵ��
��1�������Իع鷽��![]() ����ȷ��0.01����
����ȷ��0.01����
��2����![]() ���ӵ�ʱ������
���ӵ�ʱ������![]() ��Ϊ��Ч�˶����ݣ��ִ���6��ʱ������
��Ϊ��Ч�˶����ݣ��ִ���6��ʱ������![]() ����ȡ3�������ȡ��3������ǡ������Ϊ��Ч�˶����ݵĸ��ʡ�
����ȡ3�������ȡ��3������ǡ������Ϊ��Ч�˶����ݵĸ��ʡ�
�ο����ݣ�![]() ��
��
�ο���ʽ�� ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ��λԲ��Բ�ĵij�ʼλ���ڣ�0��1������ʱԲ��һ��P��λ���ڣ�0��0����Բ��x�����������������Բ������Բ��λ�ڣ�2��1��ʱ�� ![]() ������Ϊ ��
������Ϊ �� 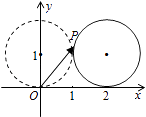
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����0��x��![]() ������y��x��3��2x�������ֵ��
������y��x��3��2x�������ֵ��
��2�������x�IJ���ʽx2-��a+1��x+a��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��˾�����![]() ��������������ѧ�ͽ̿��飩���Ⱥ�����
��������������ѧ�ͽ̿��飩���Ⱥ�����![]() ����������
����������![]() �����ձ���
�����ձ���![]() ������̫�˵�
������̫�˵�![]() ���ٵö࣬���������˾��������ٵĹ��ҡ�������۶ϱ�����ý�巴������.��������ͳ�ƽ���������������εģ����Һ�����������ȣ��ҹ�������Ķ������֮�ͣ�Ҳ���ҹ��Ǵ�ͳ�������Ź�������֮��ĵ�λ�����.ijС��Ϊ�����С������Ա�Ķ�����Ȥ���ؾٰ����������һ�������鼮�ḻС��ͼ��վ�����ڲ�ͬ������迴��ͬ���͵��鼮��Ϊ�˺����䱸��Դ���ֶ�С���ڿ�����Ա����������飬�����ȡ��һ��
���ٵö࣬���������˾��������ٵĹ��ҡ�������۶ϱ�����ý�巴������.��������ͳ�ƽ���������������εģ����Һ�����������ȣ��ҹ�������Ķ������֮�ͣ�Ҳ���ҹ��Ǵ�ͳ�������Ź�������֮��ĵ�λ�����.ijС��Ϊ�����С������Ա�Ķ�����Ȥ���ؾٰ����������һ�������鼮�ḻС��ͼ��վ�����ڲ�ͬ������迴��ͬ���͵��鼮��Ϊ�˺����䱸��Դ���ֶ�С���ڿ�����Ա����������飬�����ȡ��һ��![]() �������߽��е��飬�����ǵ�����ֳ�
�������߽��е��飬�����ǵ�����ֳ�![]() �Σ�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.�ʣ�
��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.�ʣ�

��1����������![]() ��������������ֲ���
��������������ֲ���![]() ��������
��������
��2������![]() �������������ƽ��������λ����
�������������ƽ��������λ����
��3������������![]() �Ķ���������ȡ
�Ķ���������ȡ![]() ������������������������
������������������������![]() ������ǡΪ
������ǡΪ![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() (
(![]() Ϊʵ����)��
Ϊʵ����)��

��1����![]() ʱ������
ʱ������![]() ��ͼ��д�����ĵ����������䣻
��ͼ��д�����ĵ����������䣻
��2����![]() ������
������![]() ����СֵΪ
����СֵΪ![]() ����
����![]() �ı���ʽ��
�ı���ʽ��
��3����![]() ��������
��������![]() ������
������![]() ��������������ʵ��
��������������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ƽ��ABCD����
ƽ��ABCD����![]() ��
��![]() ��
��![]() ��M��N�ֱ�Ϊ��PC��PB���е�.
��M��N�ֱ�Ϊ��PC��PB���е�.

��1��֤����A��D��M��N�ĵ㹲�棬��![]() ƽ��ADMN��
ƽ��ADMN��
��2����ֱ��BD��ƽ��ADMN���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABC��A��B��C�䣬��BAC=90�㣬AB=AC=��AA�䣬��M��N�ֱ�ΪA��B��B��C����е㣮
��1��֤����MN��ƽ��A��ACC�䣻
��2���������A�䩁MN��CΪֱ����ǣ���˵�ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com