Question

（文）将边长为的正方形沿对角线折起，使得平面平面，在折起后形成的三棱锥中，给出下列三个命题：
①是等边三角形； ②； ③三棱锥的体积是.
其中正确命题的序号是______          ___。（写出所有正确命题的序号）

Answer 1

① ②

解析试题分析：设正方形的边长为1，那么可知AC=,取AC的中点E，那么连接DE,BE,那么可知DE=BE=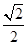,那么根据题意由于平面平面，则可知DEAC，则DE平面ABC，，故角DEB为直角，因此由勾股定理可知BD=1,BC=CD=DB=1,因此①是等边三角形正确。同时由于DEAC, BEAC,可知AC平面BDE，因此可知ACBD,故 ②成立，而三棱锥的体积可以转化为以三角形BDE为底面，高为AC的两个小三棱锥的和，那么可知为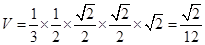,故正确的序号为① ②。
考点：本试题考查了三棱锥中的线线位置关系，以及体积的运用。
点评：解决该试题的关键是理解折叠图前后的不变量，以及垂直的关系。同时能利用等体积法思想求解几何体的体积，属于中档题。