已知集合P={x|2x2-3x+1≤0},Q={x|(x-a)(x-a-1)≤0}.
(1)若a=1,求P∩Q;
(2)若x∈P是x∈Q的充分条件,求实数a的取值范围.
【答案】
分析:(1)先解不等式求出集合P和集合Q,再根据交集的定义求出P∩Q;
(2)先将集合Q进行化简,根据x∈P是x∈Q的充分条件,得到P⊆Q,根据集合P是集合Q的子集建立不等关系,解之即可.
解答:解:(1)
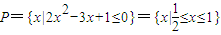
(2分)
当a=1时,Q={x|(x-1)(x-2)≤0}={x|1≤x≤2}(4分)
则P∩Q={1}(6分)
(2)∵a≤a+1,∴Q={x|(x-a)(x-a-1)≤0}={x|a≤x≤a+1}(8分)
∵x∈P是x∈Q的充分条件,∴P⊆Q(9分)
∴

,即实数a的取值范围是
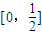
(12分)
点评:本题属于以不等式为依托,求集合的交集的基础题,以及充分条件的运用,也是高考常会考的题型.

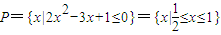 (2分)
(2分) ,即实数a的取值范围是
,即实数a的取值范围是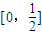 (12分)
(12分)
