
若椭圆C1: +
+ =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于 ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
(Ⅰ)求抛物线C2的方程;
(Ⅱ)若过M(-1,0)的直线l与抛物线C2交于E、F两点,又过E、F作抛物线C2的切线l1、l2,当l1⊥l2时,求直线l的方程.
(Ⅰ)已知椭圆的长半轴长为a=2,半焦距c,
由离心率e=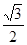 得,b2=1.
得,b2=1.
∴椭圆的上顶点为(0,1),即抛物线的焦点为(0,1),
∴p=2,抛物线的方程为x2=4y.
(Ⅱ)由题知直线l的斜率存在且不为零,则可设直线l的方程为y=k(x+1),E(x1,y1),F(x2,y2),
∵y=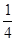 x2,∴y′=
x2,∴y′=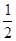 x,
x,
∴切线l1,l2的斜率分别为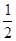 x1,
x1,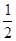 x2,
x2,
当l1⊥l2时,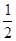 x1·
x1·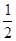 x2=-1,即x1·x2=-4,
x2=-1,即x1·x2=-4,
得:x2-4kx-4k=0,
由Δ=(-4k)2-4×(-4k)>0,解得k<-1或k>0.
又x1·x2=-4k=-4,得k=1.
∴直线l的方程为x-y+1=0.
【解析】略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:学习周报 数学 人教课标高二版(A选修1-1) 2009-2010学年 第26期 总第182期 人教课标版(A选修1-1) 题型:044
已知A(![]() ,0),B(
,0),B(![]() ,-
,-![]() )两点在椭圆C1:
)两点在椭圆C1:![]() +
+![]() =1(a>b>0)上,若椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直l1于点P,线段PF2垂直平分线交l2于点M,求点M的轨迹C2的方程.
=1(a>b>0)上,若椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直l1于点P,线段PF2垂直平分线交l2于点M,求点M的轨迹C2的方程.
查看答案和解析>>
科目:高中数学 来源:山东济宁梁山二中2011-2012学年高二12月月考数学理科试题 题型:044
若椭圆C1:![]() +
+![]() =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于![]() ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
(Ⅰ)求抛物线C2的方程;
(Ⅱ)若过M(-1,0)的直线l与抛物线C2交于E、F两点,又过E、F作抛物线C2的切线l1、l2,当l1⊥l2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:福建省四地六校2011-2012学年高二上学期第二次月考数学文科试题 题型:022
若椭圆C1:![]() +
+![]() =1(a1>b1>0)和椭圆C2:
=1(a1>b1>0)和椭圆C2:![]() +
+![]() =1(a2>b2>0)的焦点相同且a1>a2.给出如下四个结论:
=1(a2>b2>0)的焦点相同且a1>a2.给出如下四个结论:
①椭圆C1和椭圆C2一定没有公共点;
②![]() >
>![]() ;
;
③![]() ;
;
④a1-a2<b1-b2.
其中,所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试浙江卷文数 题型:013
如图F1、F2是椭圆C1∶![]() +y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是
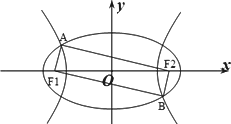
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com