
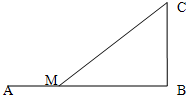
 如图,设铁路AB长为80,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为80,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.| 100+x2 |
| 100+x2 |
| 4x | ||
|
| 10 | ||
|
| 10 | ||
|
| 10 | ||
|
| 10 | ||
|
| 10 | ||
|
| 10 | ||
|


科目:高中数学 来源: 题型:解答题
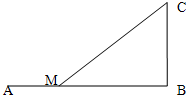 如图,设铁路AB长为80,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
如图,设铁路AB长为80,BC⊥AB,且BC=10,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.查看答案和解析>>
科目:高中数学 来源: 题型:
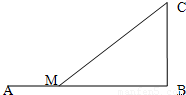
在长为100千米的铁路线AB旁的C处有一个工厂,工厂与铁路的距离CA为20千米.由铁路上的B处向工厂提供原料,公路与铁路每吨千米的货物运价比为5∶3,为节约运费,在铁路的D处修一货物转运站,设AD距离为x千米,沿CD直线修一条公路(如图).

(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省?
查看答案和解析>>
科目:高中数学 来源:2008-2009学年广东省广州六中高二(下)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com