Question

【题目】某校届高三文（1）班在一次数学测验中，全班名学生的数学成绩的频率分布直方图如下，已知分数在的学生数有人.

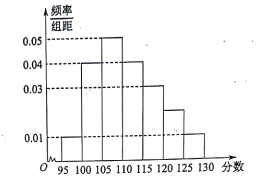
（1）求总人数和分数在的人数；

（2）利用频率分布直方图，估算该班学生数学成绩的众数和中位数各是多少？

（3）现在从比分数在名学生（男女生比例为）中任选人，求其中至多含有名男生的概率.

Answer 1

【答案】（1）;（2）， ;（3）.

【解析】试题分析：（1）根据频率分布图求分数在的频率0.35，根据公式总人数频率=频数，再计算分数在的频率，再根据总人数求分数在的人数；（2）众数是最高的小矩形的底边的中点值，中位数是中位数两边的面积分别是；（3）首先计算分数在115~120的学生有6人，其中男生2人，女生4人，给这6人编号，列举所有任选2人的基本事件的个数，以及其中至多有1名男生的基本事件的个数，并求其概率.

试题解析：（1）分数在内的学生的频率为，

所以该班总人数为.

分数在内的学生的频率为：

，

分数在内的人数为.

（2）由频率直方图可知众数是最高的小矩形底边中点的横坐标，

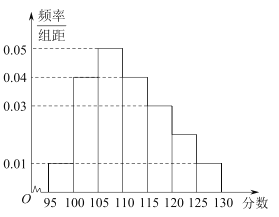
即为.

设中位数为，∵，∴.

∴众数和中位数分别是， .

（3）由题意分数在内有学生名，其中男生有名.

设女生为，男生为，从名学生中选出名的基本事件为：

共种，其中至多有名男生的基本事件共种，

∴所求的概率为.