
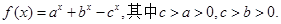
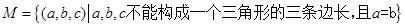 ,则
,则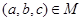 所对应的
所对应的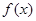 的零点的取值集合为 .
的零点的取值集合为 .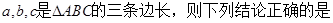 ______.(写出所有正确结论的序号)
______.(写出所有正确结论的序号)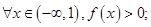
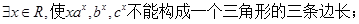
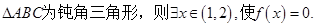
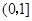 ,(2)①②③;
,(2)①②③;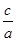 ≥2,则ln
≥2,则ln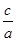 ≥ln2>0.
≥ln2>0.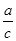 )x?1]=0.得(
)x?1]=0.得(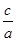 )x=2,
)x=2,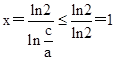 ,所以0<x≤1.
,所以0<x≤1.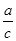 )x+(
)x+(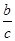 )x?1],
)x?1],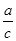 <1,
<1,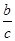 <1,所以对?x∈(-∞,1),(
<1,所以对?x∈(-∞,1),(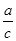 )x+(
)x+(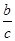 )x?1>(
)x?1>(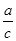 )1+(
)1+(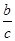 )1?1
)1?1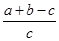 >0.所以命题①正确;
>0.所以命题①正确;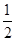 ,bx=
,bx=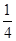 ,cx=
,cx=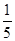 .不能构成一个三角形的三条边长.
.不能构成一个三角形的三条边长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
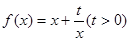 和点
和点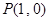 ,过点
,过点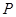 作曲线
作曲线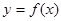 的两条切线
的两条切线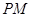 、
、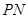 ,切点分别为
,切点分别为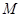 、
、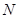 .
.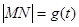 ,试求函数
,试求函数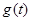 的表达式;
的表达式;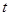 ,使得
,使得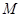 、
、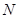 与
与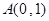 三点共线.若存在,求出
三点共线.若存在,求出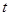 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.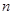 ,在区间
,在区间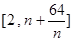 内总存在
内总存在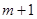 个实数
个实数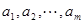 ,
,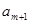 ,使得不等式
,使得不等式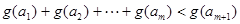 成立,求
成立,求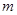 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com