
【题目】(2017·郑州第二次质量预测)如图,高为1的等腰梯形ABCD中,AM=CD=![]() AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.

(1)在AB边上是否存在点P,使AD∥平面MPC?
(2)当点P为AB边的中点时,求点B到平面MPC的距离.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1) 连接BD交MC于点N,则![]() ,因此AP=
,因此AP=![]() AB ,再根据线面平行判定定理得结论(2)利用等体积法
AB ,再根据线面平行判定定理得结论(2)利用等体积法![]() ,再根据AM⊥平面MBCD,得
,再根据AM⊥平面MBCD,得![]() ,最后计算三角形面积代入可得结果
,最后计算三角形面积代入可得结果
试题解析:解:(1)当AP=![]() AB时,有AD∥平面MPC.
AB时,有AD∥平面MPC.

理由如下:
连接BD交MC于点N,连接NP.
在梯形MBCD中,DC∥MB,![]() =
=![]() =
=![]() ,
,
在△ADB中,![]() =
=![]() ,∴AD∥PN.
,∴AD∥PN.
∵AD平面MPC,PN平面MPC,
∴AD∥平面MPC.
(2)∵平面AMD⊥平面MBCD,平面AMD∩平面MBCD=DM,AM⊥DM,∴AM⊥平面MBCD.
∴VPMBC=![]() ×S△MBC×
×S△MBC×![]() =
=![]() ×
×![]() ×2×1×
×2×1×![]() =
=![]() .
.
在△MPC中,MP=![]() AB=
AB=![]() ,MC=
,MC=![]() ,
,
又PC=![]() =
=![]() ,
,
∴S△MPC=![]() ×
×![]() ×
×![]() =
=![]() .
.
∴点B到平面MPC的距离为
d=![]() =
=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
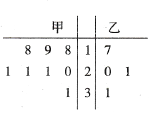
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )

A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.
AB=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC.

(1)求证:AD⊥平面BCD;
(2)求三棱锥CABD的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() ,且经过点
,且经过点![]() ,
, ![]() 轴.
轴.
(1)求椭圆![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两不同点,在椭圆
两不同点,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使四边形
,使四边形![]() 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com