
【题目】已知函数f(x)=(![]() )x.
)x.
(Ⅰ)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值g(a);
(Ⅱ)在(Ⅰ)的条件下,是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由.
【答案】(Ⅰ)g(a)=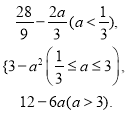 (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)在![]() 的情况下,求出
的情况下,求出![]() 的值域,对所给函数进行配方化简,可利用一元二次函数的性质对
的值域,对所给函数进行配方化简,可利用一元二次函数的性质对![]() 进行分类讨论,可得函数的最小值
进行分类讨论,可得函数的最小值![]() ;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在
;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在![]() 的单调性,结合区间与值域,可得关于
的单调性,结合区间与值域,可得关于![]() 的等式,解得
的等式,解得![]() 存在情况.
存在情况.
试题解析:(Ⅰ)∵x∈[﹣1,1],∴f(x)=(![]() )x∈[
)x∈[![]() ,3],
,3],
y=[f(x)]2﹣2af(x)+3=[(![]() )x]2﹣2a(
)x]2﹣2a(![]() )x+3
)x+3
=[(![]() )x﹣a]2+3﹣a2. .
)x﹣a]2+3﹣a2. .
由一元二次函数的性质分三种情况:
若a<![]() ,则当
,则当![]() 时,ymin=g(a)=
时,ymin=g(a)=![]() ;
;
若![]() ≤a≤3,则当
≤a≤3,则当![]() 时,ymin=g(a)=3﹣a2;
时,ymin=g(a)=3﹣a2;
若a>3,则当![]() 时,ymin=g(a)=12﹣6a.
时,ymin=g(a)=12﹣6a.
∴g(a)=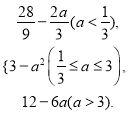
(Ⅱ)假设存在满足题意的m、n,
∵m>n>3,且g(x)=12﹣6x在区间(3,+∞)内是减函数,
又g(x)的定义域为[n,m],值域为[n2,m2],
∴![]()
两式相减,得6(m﹣n)=(m+n)(m﹣n),
∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,
∴满足题意的m、n不存在.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上, ![]() 是
是![]() 的中点,证明:
的中点,证明: ![]() ;
;
(2)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
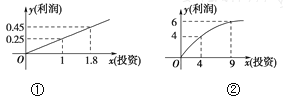
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln2x-2aln(ex)+3,x∈[e-1,e2]
(1)当a=1时,求函数f(x)的值域;
(2)若f(x)≤-alnx+4恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A﹣DF﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]() 在第一象限的交点为
在第一象限的交点为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的右顶点,
为椭圆的右顶点, ![]() 的面积为
的面积为![]() .
.
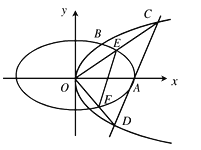
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线
点作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点,记
两点,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com