Question

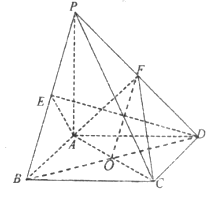
【题目】已知四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，E，F分别是PB,PD的中点．

（I）求证：PB∥平面FAC；

（II）求三棱锥P-EAD的体积；

（III）求证：平面EAD⊥平面FAC．

Answer 1

【答案】（1）见解析（2）（3）见解析

【解析】分析：（1）连接BD，与AC交于点O，连接OF，推导出OF∥PB，由此能证明PB//平面FAC；

（2）由PA⊥平面ABCD，知为棱锥的高，由，知，由此能求出结果；

（3）推导出，从而平面，进而平面，由此能证明平面平面.

详解：（I）连接BD，与AC交于点O，连接OF，

在△PBD中，O，F分别是BD，PD中点，

所以OF∥PB，

又因为OF平面FAC， PB平面FAC，

所以PB//平面FAC，

（II）法1：因为PA⊥平面ABCD，AB,AD平面ABCD，

所以PA⊥AB，PA⊥AD，

又因为AB⊥AD，，PA,AB平面PAB，

所以AD⊥平面PAB，

在直角△PAB中，PA=AB=2，E为PB中点，

所以，

所以三棱锥P-EAD的体积为．

法2：因为PA⊥平面ABCD，所以PA为棱锥P-ABD的高．

因为PA=AB=2，底面ABCD是正方形，

所以，

因为E为PB中点，所以，

所以．

（III）证明：

因为AD⊥平面PAB，PB平面PAB，

所以AD⊥PB，

在等腰直角△PAB中，AE⊥PB，

又，AE,AD平面EAD，

所以PB⊥平面EAD，

又OF∥PB，

所以OF⊥平面EAD，

又OF平面FAC，

所以平面EAD⊥平面FAC．