C
分析:由已知数列{a
n}是等差数列,a
1=1,d≠0可以表示出a
3,a
4,a
6,再根据a
3,a
4,a
6是一个等比数列的前3项,即可求出d,进而可得出等比数列的首项与公比,即可求出第四项.
解答:∵数列{a
n}是等差数列,a
1=1,∴a
3=1+2d,a
4=1+3d,a
6=1+5d.
∵a
3,a
4,a
6是一个等比数列{b
n}的前3项,∴
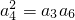
,
∴(1+3d)
2=(1+2d)(1+5d),
化为d
2+d=0,解得d=0,d=-1,
∵d≠0,∴d=-1.
∴a
3=1-2=-1=b
1,a
4=1-3=-2=b
2,
公比q=
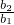
=

=

=2.
∴这一等比数列的第4项b
4=b
1q
3=-1×2
3=-8.
故选C.
点评:熟练掌握等差数列与等比数列的定义与通项公式是解题的关键.

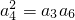 ,
,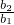 =
= =
= =2.
=2.

 智慧小复习系列答案
智慧小复习系列答案