
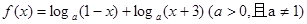
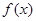 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数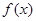 有最小值为
有最小值为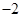 ,求
,求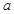 的值。
的值。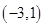 ,当
,当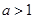 时,值域为
时,值域为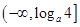 ,当
,当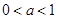 时,值域为
时,值域为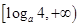 ;
;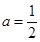
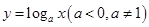 的定义域为
的定义域为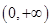 ,则由函数
,则由函数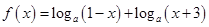 ,可得
,可得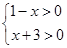 ,解之得
,解之得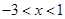 ,从而可得所求函数的定义域为
,从而可得所求函数的定义域为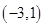 ;根据对数函数
;根据对数函数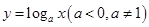 当
当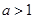 时为单调递增函数,当
时为单调递增函数,当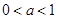 时为单调递减函数,又由复合函数的“同增异减”性质(注:两个复合函数的单调性相同时复合函数为单调递增,不同时复合函数为单调递减),可将函数
时为单调递减函数,又由复合函数的“同增异减”性质(注:两个复合函数的单调性相同时复合函数为单调递增,不同时复合函数为单调递减),可将函数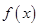 对其底数
对其底数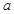 分为
分为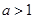 与
与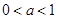 两情况进行分类讨论,从而求出函数
两情况进行分类讨论,从而求出函数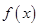 的值域;(2)由(1)知当
的值域;(2)由(1)知当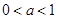 时函数
时函数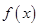 有最小值,从而有
有最小值,从而有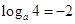 ,可解得
,可解得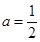 .
.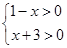 ,解之得
,解之得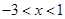 ,故所求函数的定义域为
,故所求函数的定义域为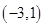 .
.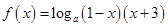 ,设
,设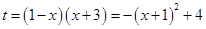 ,又
,又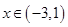 ,所以
,所以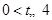 .
.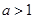 时,有
时,有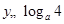 ;当
;当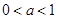 时,
时, 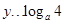 .
.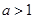 时,函数
时,函数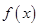 的值域为
的值域为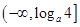 ,当
,当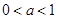 时,值域为
时,值域为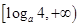 .
.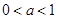 时,函数有最小值,即
时,函数有最小值,即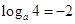 ,可解得
,可解得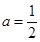 .
.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com