
【题目】已知球内接正四棱锥![]() 的高为
的高为![]() 相交于
相交于![]() ,球的表面积为
,球的表面积为![]() ,若
,若![]() 为
为![]() 中点.
中点.
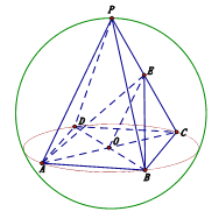
(1)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1) 由球的表面积求出球的半径R,设球心为![]() ,则
,则![]() 必在
必在![]() 上,连
上,连![]() ,根据球的性质有
,根据球的性质有![]() ,求解易得底面边长以及侧棱长,则结论易得;(2)证明
,求解易得底面边长以及侧棱长,则结论易得;(2)证明![]() 平面
平面![]() ,则
,则![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,由
的距离,由![]() ,则结论易得.
,则结论易得.
试题解析:由球的表面积公式![]() ,得球的半径
,得球的半径![]() ,
,
设球心为![]() ,在正四棱锥
,在正四棱锥![]() 中,高为
中,高为![]() ,则
,则![]() 必在
必在![]() 上,
上,
连![]() ,则
,则![]() ,
,
则在![]() ,有
,有![]() ,即
,即![]() ,可得正方形
,可得正方形![]() 的边长为
的边长为![]() ,
,
侧棱![]() .
.
(1)在正方形![]() 中,
中, ![]() ,所
,所![]() 以是异面直线
以是异面直线![]() 和
和![]() 所成的角或其补角,
所成的角或其补角,
取![]() 中点
中点![]() ,在等腰
,在等腰![]() 中,可得
中,可得![]() ,斜高
,斜高![]() ,
,
则在![]() 中,
中, ![]() ,
,
所以异面直线![]() 和
和![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;
;
(2)由![]() 为
为![]() 中点,得
中点,得![]() ,
,
且满足![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,
的距离,
又因为![]() ,
,
再设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() ,
,
可得![]() ,则
,则![]() ,
,
所以点![]() 到平面
到平面![]() 的距离
的距离![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心和抛物线
的中心和抛物线![]() 的顶点都在坐标原点
的顶点都在坐标原点![]() ,
, ![]() 和
和![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 的长轴长、短轴长及点
的长轴长、短轴长及点![]() 到直线
到直线![]() 的距离成等比数列。
的距离成等比数列。
(Ⅰ)当![]() 的准线与直线
的准线与直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 及
及![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,交
两点,交![]() 于
于![]() ,
, ![]() 两点。当
两点。当![]() 时,求
时,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
,从中抽取![]() 人作为调查对象,得到了如图所示的这
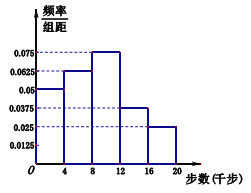
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x(2﹣k)(1+k)(k∈Z),且f(x)在(0,+∞)上单调递增.
(1)求实数k的值,并写出相应的函数f(x)的解析式;
(2)试判断是否存在正数q,使函数g(x)=1﹣qf(x)+(2q﹣1)x在区间[﹣1,2]上的值域为[﹣4, ![]() ].若存在,求出q的值;若不存在,请说明理由.
].若存在,求出q的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且在(0,+∞)是增函数,又f(﹣3)=0,则不等式xf(x)≥0的解集是( )
A.{x|﹣3≤x≤3}
B.{x|﹣3≤x<0或0<x≤3}
C.{x|x≤﹣3或x≥3}
D.{x|x≤﹣3或x=0或x≥3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,将曲线
中,将曲线 (
(![]() 为参数)上每一点的横坐标保持不变,纵坐标变为原来的2倍,得到曲线
为参数)上每一点的横坐标保持不变,纵坐标变为原来的2倍,得到曲线![]() ;以坐标原点
;以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com