
【题目】正整数数列![]() 满足:
满足:![]() ,
,![]() .试求通项公式
.试求通项公式![]() .
.
【答案】![]()
【解析】
据条件![]() 知,数列严格递增.于是,
知,数列严格递增.于是,![]()
先在条件式中取![]() ,得到
,得到![]() ,
,
即![]() . ①
. ①
据式①左端得![]() .
.
则![]() . ②
. ②
又由式①右端得![]() ,且
,且![]() ,
,
故![]() . ③
. ③
据式②、③得整数![]() .
.
再对条件式中取![]() ,得到
,得到![]() ,
,
即![]() . ④
. ④
由式④左端得![]() .
.
则![]() .
.
由式④右端得![]() ,即
,即![]() .
.
因![]() ,所以,
,所以,![]() .故
.故![]() .
.
继而在已知式中取![]() ,得
,得![]() ,
,
即![]() . ⑤
. ⑤
又![]() 为正整数,故式⑤右端恒成立.
为正整数,故式⑤右端恒成立.
而由式⑤左端有![]() ,故
,故![]() ,得
,得![]() .
.
由![]() ,
,![]() ,
,![]() ,
,![]() ,猜想
,猜想![]() . ⑥
. ⑥
首先,若将式⑥代入已知式得![]() ,
,
即![]() ,或
,或![]() .
.
此式显然成立.
下证:![]() 是满足条件的唯一数列.
是满足条件的唯一数列.
对![]() 归纳.当
归纳.当![]() 时已验证.若式⑥对于
时已验证.若式⑥对于![]() 成立,则对于
成立,则对于![]() ,据已知式有
,据已知式有
![]() . ⑦
. ⑦
由式⑦右端得![]() .
.
则![]() . ⑧
. ⑧
(这里用到,当![]() 时,
时,![]()
![]()
![]() .)
.)
据式⑦左端得![]() ,
,
即![]() . ⑨
. ⑨
其判别式![]()
![]()
![]()
![]() .
.
设与式⑨对应的关于![]() 的一元二次方程的两根为
的一元二次方程的两根为![]() 、
、![]() .
.
则![]()
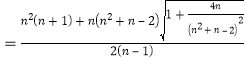
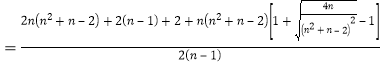
![]()
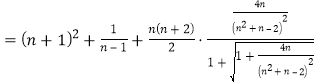
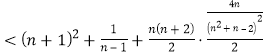
![]()
![]() . ⑩
. ⑩
(这里用到,当![]() 时,
时,![]()
![]()
![]() .)
.)
据式⑧、⑩得![]() .
.
故由归纳法知,对任意的![]() ,式⑥成立,即
,式⑥成立,即![]() .
.


科目:高中数学 来源: 题型:
【题目】设抛物线的顶点为A,焦点为F.过F作直线l与抛物线交于点P、Q,直线AP、AQ分别与抛物线的准线交于点M、N.问:直线l满足什么条件时,三直线PN、QM、AF恒交于一点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: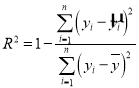 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
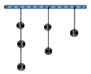
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次比赛中,某队的六名队员均获得奖牌,共获得4枚金牌2枚银牌,在颁奖晚会上,这六名队员与1名领队排成一排合影,若两名银牌获得者需站在领队的同侧,则不同的排法共有______种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体。在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱,拱与拱之间垫的方形木块叫斗。如图所示,是“散斗”(又名“三才升”)的三视图,则它的体积为( )

A. ![]() B.
B. ![]() C. 53 D.
C. 53 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF![]() a,以下结论正确的有( )
a,以下结论正确的有( )

A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的![]()
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com