
函数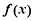 定义在区间
定义在区间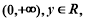 都有
都有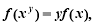 且
且 不恒为零.
不恒为零.
(1)求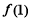 的值;
的值;
(2)若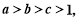 且
且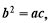 求证:
求证: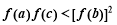 ;
;
(3)若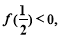 求证:
求证: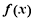 在
在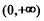 上是增函数.
上是增函数.
(1)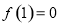 .(2)(3)见解析
.(2)(3)见解析
【解析】
试题分析:(1)通过带特殊值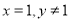 可求得;(2)设
可求得;(2)设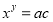 ,同取以
,同取以 为底的对数得
为底的对数得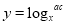 ,
,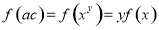 ,把
,把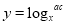 代入在运用对数运算性质就可得
代入在运用对数运算性质就可得 ,有
,有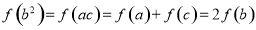 ,所以
,所以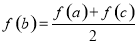 ,要证
,要证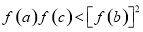 只需证
只需证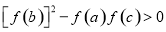 ,由以上很容易得到
,由以上很容易得到 ,需要证出
,需要证出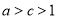 时,
时,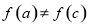 即等号不成立;(3)设
即等号不成立;(3)设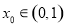 ,则
,则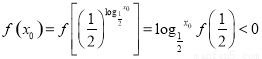 ,所以得
,所以得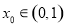 时,
时,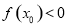 ,任取
,任取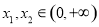 ,
,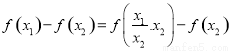 得证.
得证.
试题解析:⑴令 ,
,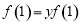 ,
,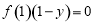 ,
,
因为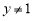 ,所以
,所以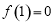 . 3分
. 3分
⑵设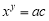 ,则
,则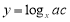 ,所以
,所以

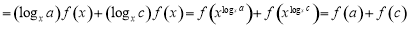 , 5分
, 5分
因为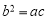 ,所以
,所以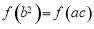 ,所以
,所以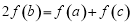 ,
,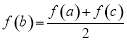 ,
,
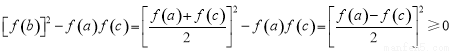 . 8分
. 8分
下面证明当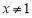 时,
时,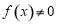 .
.
假设存在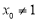 ,
,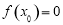 ,则对于任意
,则对于任意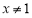 ,
,
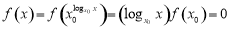 ,不合题意.所以,当
,不合题意.所以,当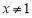 时,
时,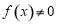 .
.
因为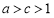 ,所以存在
,所以存在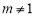 ,
,
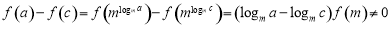 ,
,
所以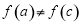 ,所以
,所以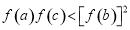 . 10分
. 10分
⑶设 ,则
,则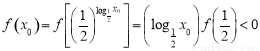 , 12分
, 12分
设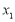 ,
,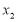 为区间
为区间 内的任意两个值,且
内的任意两个值,且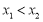 ,则
,则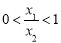 ,由⑵的证明知,
,由⑵的证明知,
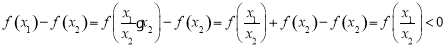 ,
,
所以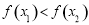 ,所以
,所以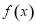 在
在 上是增函数. 16分
上是增函数. 16分
考点:1.函数附特殊值法;2.函数的构造法;3.证明单调函数.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2016届江苏省扬州市高一上学期期末调研测试数学试卷(解析版) 题型:填空题
将函数 的图象先向右平移
的图象先向右平移 个单位,再将得到的图象上各点的横坐标变为原来的
个单位,再将得到的图象上各点的横坐标变为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象,若
的图象,若 ,则函数
,则函数 的值域为 .
的值域为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com