
【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 |
|
税率 | 3 | 10 | 20 | 25 |
|
(1)现有李某月收入29600元,膝下有一名子女,需要赡养老人,除此之外,无其它专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)为研究月薪为20000元的群体的纳税情况,现收集了某城市500名的公司白领的相关资料,通过整理资料可知,有一个孩子的有400人,没有孩子的有100人,有一个孩子的人中有300人需要赡养老人,没有孩子的人中有50人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的500人中,任何两人均不在一个家庭).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群缴纳个税金额![]() 的分布列与期望.
的分布列与期望.
【答案】(1)李某月应缴纳的个税金额为![]() 元,(2)分布列详见解析,期望为1150元
元,(2)分布列详见解析,期望为1150元
【解析】
(1)分段计算个人所得税额;
(2)随机变量X的所有可能的取值为990,1190,1390,1590,分别求出各值对应的概率,列出分布列,求期望即可.
解:(1)李某月应纳税所得额(含税)为:29600500010002000=21600元
不超过3000的部分税额为3000×3%=90元
超过3000元至12000元的部分税额为9000×10%=900元,
超过12000元至25000元的部分税额为9600×20%=1920元
所以李某月应缴纳的个税金额为90+900+1920=2910元,
(2)有一个孩子需要赡养老人应纳税所得额(含税)为:20000500010002000=12000元,
月应缴纳的个税金额为:90+900=990元
有一个孩子不需要赡养老人应纳税所得额(含税)为:2000050001000=14000元,
月应缴纳的个税金额为:90+900+400=1390元;
没有孩子需要赡养老人应纳税所得额(含税)为:2000050002000=13000元,
月应缴纳的个税金额为:90+900+200=1190元;
没有孩子不需要赡养老人应纳税所得额(含税)为:200005000=15000元,
月应缴纳的个税金额为:90+900+600=1590元;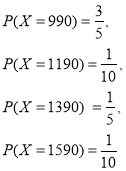 .
.
所以随机变量X的分布列为:
| 990 | 1190 | 1390 | 1590 |
|
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.
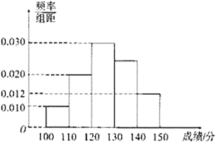
(1)求第四个小矩形的高;
(2)估计本校在这次统测中数学成绩不低于120分的人数;
(3)已知样本中,成绩在![]() 内的有两名女生,现从成绩在这个分数段的学生中随机选取2人做学习交流,求恰好男生女生各有一名的概率.
内的有两名女生,现从成绩在这个分数段的学生中随机选取2人做学习交流,求恰好男生女生各有一名的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”,收集了使用该型号电动汽车![]() 年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
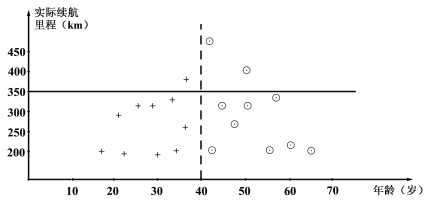
注:“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值.
(Ⅰ)记A,B两组客户的电动汽车的“实际平均续航里程数”的平均值分别为![]() ,
,![]() ,根据图中数据,试比较
,根据图中数据,试比较![]() ,
,![]() 的大小(结论不要求证明);
的大小(结论不要求证明);
(Ⅱ)从A,B两组客户中随机抽取2位,求其中至少有一位是A组的客户的概率;
(III)如果客户的电动汽车的“实际平均续航里程数”不小于350,那么称该客户为“驾驶达人”.从A,B两组客户中,各随机抽取1位,记“驾驶达人”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=k(x+1)与C相切于点A,|AF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线l交C于M,N两点,T是MN的中点,若|MN|=8,求点T到y轴距离的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中
中![]() ,函数
,函数![]() .
.
(1)若正项数列![]() 满足
满足![]() ,试求出
,试求出![]() ,
, ![]() ,
, ![]() ,由此归纳出通项
,由此归纳出通项![]() ,并加以证明;
,并加以证明;
(2)若正项数列![]() 满足
满足![]() (n∈N*),数列
(n∈N*),数列![]() 的前项和为Tn,且
的前项和为Tn,且![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
两位选手,随机调查了20个学生的评分,得到下面的茎叶图:

所得分数 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
(1)通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计![]() 两位选手中哪位选手直接晋级的概率更大,并说明理由.
两位选手中哪位选手直接晋级的概率更大,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受电视机在保修期内维修费等因素的影响,企业生产每台电视机的利润与该电视机首次出现故障的时间有关.某电视机制造厂生产甲、乙两种型号电视机,保修期均为2年,现从该厂已售出的两种型号电视机中各随机抽取50台,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故障时间x(年) |
|
|
|
|
|
电视机数量(台) | 3 | 5 | 42 | 8 | 42 |
每台利润(千元) | 1 | 2 | 3 | 1.8 | 2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲种型号电视机中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)该厂预计今后这两种型号电视机销量相当,由于资金限制,只能生产其中一种型号电视机,若从经济效益的角度考虑,你认为应该产生哪种型号电视机?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com