练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线过点，且在两坐标轴上的截距相等，则此直线的方程为_____________.

    【答案】或

    【解析】

    分两种情况考虑，第一：当所求直线与两坐标轴的截距不为0时，设出该直线的方程为，把已知点坐标代入即可求出的值，得到直线的方程；第二：当所求直线与两坐标轴的截距为0时，设该直线的方程为，把已知点的坐标代入即可求出的值，得到直线的方程，综上，得到所有满足题意的直线的方程．

    解：①当所求的直线与两坐标轴的截距不为0时，设该直线的方程为，

    把代入所设的方程得：，则所求直线的方程为即；

    ②当所求的直线与两坐标轴的截距为0时，设该直线的方程为，

    把代入所求的方程得：，则所求直线的方程为即．

    综上，所求直线的方程为：或．

    故答案为：或

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

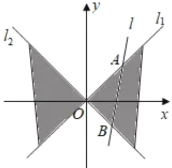
    【题目】如图，在平面直角坐标系中，直线与直线之间的阴影部分记为，区域中动点到的距离之积为1.

    （1）求点的轨迹的方程；

    （2）对于区域中动点，求的取值范围；

    （3）动直线穿过区域，分别交直线于两点，若直线与点的轨迹有且只有一个公共点，求证：的面积值为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

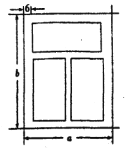
    【题目】如图，一个铝合金窗分为上、下两栏，四周框架和中间隔档的材料为铝合金，宽均为6，上栏与下栏的框内高度（不含铝合金部分）的比为1:2，此铝合金窗占用的墙面面积为28800，设该铝合金窗的宽和高分别为，铝合金窗的透光部分的面积为.

    （1）试用表示；

    （2）若要使最大，则铝合金窗的宽和高分别为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知圆A：(x＋3)2＋y2＝100，圆A内一定点B(3，0)，圆P过B且与圆A内切，则圆心P的轨迹方程为_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

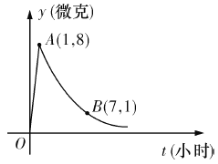
    【题目】某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用，服用药后每毫升血液中的含药量（微克）与服药的时间（小时）之间近似满足如图所示的曲线，其中是线段，曲线是函数（，，且，是常数）的图象.

    （1）写出服药后关于的函数关系式；

    （2）据测定，每毫升血液中的含药量不少于微克时治疗疾病有效.假设某人第一次服药为早上，为保持疗效，第二次服药最迟应当在当天几点钟？

    （3）若按（2）中的最迟时间服用第二次药，则第二次服药后小时，该病人每毫升血液中的含药量为多少微克？（精确到微克）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于圆周率，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验.受其启发，我们也可以通过设计下面的实验来估计的值：先请名同学，每人随机写下一个都小于1的正实数对；再统计两数能与1构成钝角三角形三边的数对的个数；最后再根据统计数来估计的值.假如统计结果是，那么可以估计（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中， 分别是的中点.

    （1）求证： 平面；

    （2）若三棱柱的体积为4，求异面直线与夹角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当，且的最大值为，求的值；

    （2）方程在上的两解分别为、，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求的定义域；

    （2）判断的奇偶性并给予证明；

    （3）求关于x的不等式的解集．

    查看答案和解析>>

    同步练习册答案