[题目]函数f(x)=x2cosx在的图象大致是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】函数f（x）=x2cosx在的图象大致是（）
A.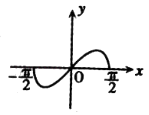
B.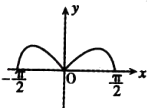
C.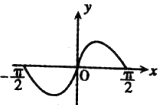
D.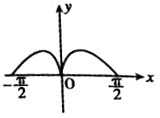

【答案】B
【解析】解：函数f（x）=x2cosx在，满足f（﹣x）=f（x），所以函数是偶函数，排除选项A，C；

当x∈（0，）时，f′（x）=2xcosx﹣x2sinx，令2xcosx﹣x2sinx=0，可得xtanx=2，方程的解x ，即函数的极大值点x ，排除D，

故选：B．

【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)，还要掌握函数的极值与导数(求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值)的相关知识才是答题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，已知四棱台上、下底面分别是边长为3和6的正方形，，且
底面，点，分别在棱，上.
(1)若是是的中点，证明：;
(2若//平面，二面角的余弦值为，求四面体的体积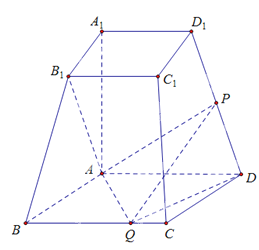

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知双曲线C： =1（b＞a＞0）的右焦点为F，O为坐标原点，若存在直线l过点F交双曲线C的右支于A，B两点，使 =0，则双曲线离心率的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=（x﹣a）ex ， a∈R．（Ⅰ）当a=1时，试求f（x）的单调增区间；
（Ⅱ）试求f（x）在[1，2]上的最大值；
（Ⅲ）当a=1时，求证：对于x∈[﹣5，+∞），恒成立．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图1，在Rt△ABC中，∠C=90°，AC=4，BC=2，D，E分别为边AC，AB的中点，点F，G分别为线段CD，BE的中点．将△ADE沿DE折起到△A1DE的位置，使∠A1DC=60°．点Q为线段A1B上的一点，如图2．
（Ⅰ）求证：A1F⊥BE；
（Ⅱ）线段A1B上是否存在点Q使得FQ∥平面A1DE？若存在，求出A1Q的长，若不存在，请说明理由；
（Ⅲ）当时，求直线GQ与平面A1DE所成角的大小．