
(1)求点P的轨迹方程.
(2)当t=![]() 时,是否存在直线l,使l是椭圆与(1)中轨迹的公切线?若存在,求出l的方程;若不存在,请说明理由.
时,是否存在直线l,使l是椭圆与(1)中轨迹的公切线?若存在,求出l的方程;若不存在,请说明理由.
解:(1)设P(x,y),∵F(2,0),∴![]() =(-x,-y),
=(-x,-y),![]() =(2-x,-y).于是
=(2-x,-y).于是![]() ·
·![]() =-x(2-x)+y2,
=-x(2-x)+y2,
即(x-1)2+y2=t+1,故点P的轨迹方程为(x-1)2+y2=t+1(t>-1).
(2)当t=-![]() 时,点P的轨迹(x-1)2+y2=
时,点P的轨迹(x-1)2+y2=![]() .
.
椭圆的左,右顶点分别为(-![]() ,0),(
,0),(![]() ,0),而圆与轴的两交点为(1-
,0),而圆与轴的两交点为(1-![]() ,0),(1+
,0),(1+![]() ,0),
,0),
∵-![]() <1-
<1-![]() ,1+
,1+![]() <
<![]() ,
,
∴垂直于x轴的直线不可能与两曲线相切.
设公切线方程为y=kx+b,由题意可得![]() =
=![]()
![]() k2+8kb+4b2-3=0,①
k2+8kb+4b2-3=0,①
把y=kx+b代入椭圆方程,得(5k2+1)x2+10kbx+5b2-5=0,由Δ=0,得-5k2+b2-1=0,即b2=5k2+1,②
将②代入①,得8kb=-21k2-1,③
②③联立,得k=±![]() ,由③知k、b异号,∴k=
,由③知k、b异号,∴k=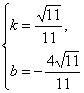 或
或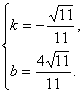
∴符合条件的直线存在,其方程为
y=![]() x
x![]() 或y=
或y=![]() x+
x+![]() .
.


科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 1 |
| 2 |
| A、(0,±2) | ||||||
| B、(0,±1) | ||||||
C、(
| ||||||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求点P的轨迹曲线C的方程;
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;
(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且![]() =-3,求a的值.
=-3,求a的值.
(文)(本小题满分12分)设函数f(x)=![]() x3+2ax2-3a2x+
x3+2ax2-3a2x+![]() a(0<a<1).
a(0<a<1).
(1)求函数f(x)的单调区间;
(2)若当x∈[a,2]时,恒有f(x)≤0,试确定实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:选择题
设椭圆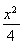 +y2=1的左焦点为F,P为椭圆上一点,其横坐标为
+y2=1的左焦点为F,P为椭圆上一点,其横坐标为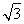 ,则|PF|等于( )
,则|PF|等于( )
(A) 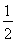 (B)
(B)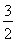 (C)
(C)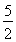 (D)
(D)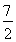
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com