
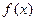 ,如果存在给定的实数对(
,如果存在给定的实数对(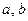 ),使得
),使得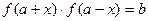 恒成立,则称
恒成立,则称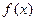 为“S-函数”.
为“S-函数”.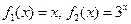 是否是“S-函数”;
是否是“S-函数”;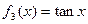 是一个“S-函数”,求出所有满足条件的有序实数对
是一个“S-函数”,求出所有满足条件的有序实数对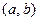 ;
; 的函数
的函数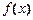 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对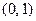 和
和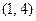 ,当
,当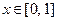 时,
时,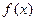 的值域为
的值域为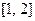 ,求当
,求当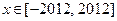 时函数
时函数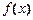 的值域.
的值域. 是一个“S-函数”的常数(a, b)=
是一个“S-函数”的常数(a, b)=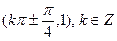
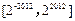
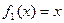 是“S-函数”,则存在常数
是“S-函数”,则存在常数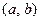 ,使得 (a+x)(a-x)=b.
,使得 (a+x)(a-x)=b.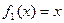 不是“S-函数”.………………………………………………3分
不是“S-函数”.………………………………………………3分
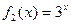 是“S-函数”,则存在常数a,b使得
是“S-函数”,则存在常数a,b使得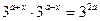 ,
,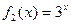 是“S-函数”………………………………………………………6分
是“S-函数”………………………………………………………6分 是一个“S-函数”,设有序实数对(a, b)满足:
是一个“S-函数”,设有序实数对(a, b)满足: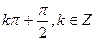 时,tan(a-x)tan(a+x)= -cot2(x),不是常数.……………………7分
时,tan(a-x)tan(a+x)= -cot2(x),不是常数.……………………7分 ,
,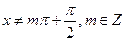 ,
, .
.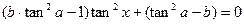 恒成立. ……………………………9分
恒成立. ……………………………9分
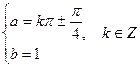 ,
,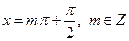 ,
, 时,tan(a-x)tan(a+x)=cot2(a)=1.
时,tan(a-x)tan(a+x)=cot2(a)=1. 是一个“S-函数”的常数(a, b)=
是一个“S-函数”的常数(a, b)=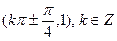 .…12分
.…12分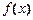 是“S-函数”,且存在满足条件的有序实数对
是“S-函数”,且存在满足条件的有序实数对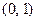 和
和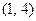 ,
,
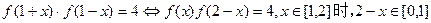 ,
,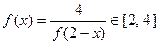 ,
,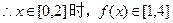 .……………………14分
.……………………14分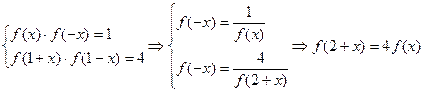 .………16分
.………16分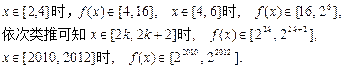
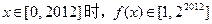 , …………………………………………17分
, …………………………………………17分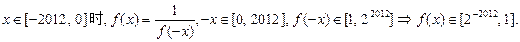
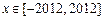 时函数
时函数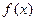 的值域为
的值域为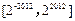 .……………18分
.……………18分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
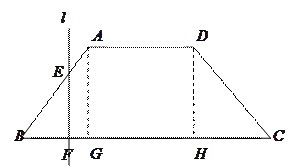
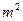 的背面靠墙的矩形小屋,房屋
的背面靠墙的矩形小屋,房屋 正面的造价为1200元/
正面的造价为1200元/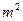 ,房屋侧面造价为800元/
,房屋侧面造价为800元/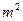 ,屋顶的总造价为5800
,屋顶的总造价为5800 元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?
元,如果墙面高为3m,且不计房屋背面费用,问怎样设计房屋能使得总造价最低,最低造价为多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com