
【题目】已知函数f(x)= ![]() (a∈R).
(a∈R).
(Ⅰ)求f(x)在区间[-1,2]上的最值;
(Ⅱ)若过点P(1,4)可作曲线y=f(x)的3条切线,求实数a的取值范围。
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:(Ⅰ)求导得到函数的单调性,根据单调性求得函数的极值和端点值,比较可得函数的最值;(Ⅱ)设切点![]() ,进而得直线
,进而得直线![]() 的斜率为
的斜率为![]() ,若曲线有3条切线,则方程
,若曲线有3条切线,则方程![]() 有3个实数根, 即方程
有3个实数根, 即方程![]() 有3个根,然后构造函数利用单调性、极值求解。
有3个根,然后构造函数利用单调性、极值求解。
试题解析:
(Ⅰ)∵ f(x)= ![]()
![]() ,
,
由![]() 解得
解得![]() 或
或![]() ;
;
由![]() 解得
解得![]() ,
,
又![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又 ![]() ,
,
∴![]() 最大值是
最大值是![]() ,最小值是
,最小值是![]() .
.
(Ⅱ) 设切点![]()
∴直线![]() 的斜率为
的斜率为
![]() ,
,
整理得![]() ,
,
由题意知此方程应有3个解.
令![]() ,
,
∴![]() ,
,
由![]() 解得
解得![]() 或
或![]() ,由
,由![]() 解得
解得![]() ,
,
∴ 函数![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴ 当![]() 时,
时, ![]() 有极大值,且极大值为
有极大值,且极大值为![]() ;
;
当![]() 时,
时, ![]() 有极小值,且极小值为
有极小值,且极小值为![]() ;
;
要使得方程![]() 有3个根,
有3个根,
则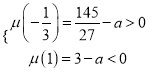 ,
,
解得![]() ,
,
∴ 实数a的取值范围为![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域是(0,+∞),且对任意的正实数x,y都有f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且x>1时,f(x)>0.
(1)求f( ![]() )的值;
)的值;
(2)判断y=f(x)在(0,+∞)上的单调性,并给出你的证明;
(3)解不等式f(x2)>f(8x﹣6)﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
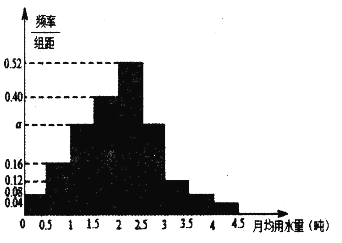
(1)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(2)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点与抛物线y2=4x的焦点F重合.
,右焦点与抛物线y2=4x的焦点F重合.
(1)求椭圆的方程;
(2)过F的直线l交椭圆于A、B两点,椭圆的左焦点力F',求△AF'B的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2(a为实常数).
(1)当a=﹣4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1 , x2∈[1,e],都有 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要100米,铁丝300米,设该厂用所有原来编制个花篮![]() ,
, ![]() 个花盆.
个花盆.
(Ⅰ)列出![]() 满足的关系式,并画出相应的平面区域;
满足的关系式,并画出相应的平面区域;
(Ⅱ)若出售一个花篮可获利300元,出售一个花盘可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,其中a∈R.
,其中a∈R.
(1)若a=1,f(x)的定义域为区间[0,3],求f(x)的最大值和最小值;
(2)若f(x)的定义域为区间(0,+∞),求a的取值范围,使f(x)在定义域内是单调减函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com