
【题目】当今世界科技迅猛发展,信息日新月异.为增强全民科技意识,提高公众科学素养,某市图书馆开展了以“亲近科技、畅想未来”为主题的系列活动,并对不同年龄借阅者对科技类图书的情况进行了调查.该图书馆从只借阅了一本图书的借阅者中随机抽取100名,数据统计如表:
借阅科技类图书(人) | 借阅非科技类图书(人) | |
年龄不超过50岁 | 20 | 25 |
年龄大于50岁 | 10 | 45 |
(1)是否有99%的把握认为年龄与借阅科技类图书有关?
(2)该图书馆为了鼓励市民借阅科技类图书,规定市民每借阅一本科技类图书奖励积分2分,每借阅一本非科技类图书奖励积分1分,积分累计一定数量可以用积分换购自己喜爱的图书.用表中的样本频率作为概率的估计值.
(i)现有3名借阅者每人借阅一本图书,记此3人增加的积分总和为随机变量ξ,求ξ的分布列和数学期望;
(ii)现从只借阅一本图书的借阅者中选取16人,则借阅科技类图书最有可能的人数是多少?
附:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(1)有99%的把握认为年龄与借阅科技类图书有关;(2)(i)分布列详见解析,数学期望为3.9;(ii)5人.
【解析】
(1)根据K2的表达式代入计算即可判断;
(2)(i)由题知借阅科技类图书的概率P![]() ,若这3人增加的积分总和为随机变量ξ,分别计算出P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),即可得到分布列及期望;
,若这3人增加的积分总和为随机变量ξ,分别计算出P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),即可得到分布列及期望;
(ii)根据题意得随机变量X满足X~B(16,![]() )的二项分布,列出不等式组,解出即可
)的二项分布,列出不等式组,解出即可
解:(1)K2![]() 8.129>6.635,
8.129>6.635,
所以有99%的把握认为年龄与借阅科技类图书有关;
(2)(i)因为用表中的样本频率作为概率的估计值,所以借阅科技类图书的概率P![]() ,
,
因为3名借阅者每人借阅一本图书,这3人增加的积分总和为随机变量ξ,
所以随机变量ξ的可能取值为3,4,5,6,
P(ξ=3)![]()
P(ξ=4)![]()
P(ξ=5)![]()
P(ξ=6)![]() ,
,
从而ξ的分布列为:
ξ | 3 | 4 | 5 | 6 |
P |
|
|
|
|
所以E(ξ)=3![]() 4
4![]() 5
5![]() 6
6![]() 3.9;
3.9;
(ii)记16人中借阅科技类图书的人数为X,则随机变量X满足二项分布X~B(16,![]() )
)
设借阅科技类图书最有可能的人数时k(k=0,1,2,……,16)
则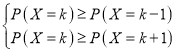 ,
,
而![]() ,
,![]() ,
,
解得4.1≤k≤5.1,
故k=5,
所以16人借阅科技类图书最有可能的人数是5人


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为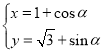 (α为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,(
,(![]() ).
).
(1)求曲线C的极坐标方程;
(2)设直线l与曲线C相交于不同的两点![]() ,
,![]() ,指出
,指出![]() 的范围,并求
的范围,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,
,![]()
(1)求椭圆离心率;
(2)点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程;
,求椭圆方程;
(3)在(2)的条件下,点![]() 在椭圆上且异于
在椭圆上且异于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,说明
,说明![]() 运动时以
运动时以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并证明.
的位置关系,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)从城市中学成绩在80分以上的学生中抽取4名,记这4名学生的成绩在90分以上的人数为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超级细菌是一种耐药性细菌,产生超级细菌的主要原因是用于抵抗细菌侵蚀的药物越来越多,但是由于滥用抗生素的现象不断的发生,很多致病菌也对相应的抗生素产生了耐药性,更可怕的是,抗生素药物对它起不到什么作用,病人会因为感染而引起可怕的炎症,高烧,痉挛,昏迷甚至死亡.某药物研究所为筛查某种超级细菌,需要检验血液是否为阳性,现有n(![]() )份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验n次;(2)混合检验,将其中k(
)份血液样本,每个样本取到的可能性相等,有以下两种检验方式:(1)逐份检验,则需要检验n次;(2)混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,则这份的血液全为阴性,因而这k份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
)份血液样本分别取样混合在一起检验,若检验结果为阴性,则这份的血液全为阴性,因而这k份血液样本只要检验一次就够了;如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).现取其中k(
).现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)运用概率统计的知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(2)若P与抗生素计量![]() 相关,其中
相关,其中![]() ,
,![]() ,…,
,…,![]() (
(![]() )是不同的正实数,满足
)是不同的正实数,满足![]() ,对任意的
,对任意的![]() (
(![]() ),都有
),都有![]() .
.
(i)证明:![]() 为等比数列;
为等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数期望值比逐份检验的总次数期望值更少,求k的最大值.
时,采用混合检验方式可以使得样本需要检验的总次数期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
![]() 若
若![]() ,
,![]() ,①若函数
,①若函数![]() 单调递增,求实数
单调递增,求实数![]() 的取值范围;②若对任意
的取值范围;②若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
![]() 若
若![]() ,且
,且![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com