
已知数列 的前
的前 项和为
项和为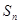 ,对一切正整数
,对一切正整数 ,点
,点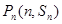 都在函数
都在函数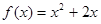 的图象上.
的图象上.
(1)求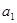 ,
,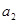 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若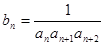 ,求证数列
,求证数列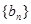 的前
的前 项和
项和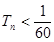 .
.
(1)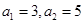 (2)
(2) (3)见解析
(3)见解析
解析试题分析:
(1)把点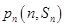 带入函数
带入函数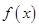 的解析式即可得到
的解析式即可得到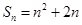 ,利用数列前n项和的定义可得
,利用数列前n项和的定义可得 ,则分别令
,则分别令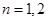 带入式子
带入式子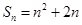 即可得到
即可得到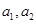 的值.
的值.
(2)由(1)可得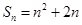 ,则利用前n项和
,则利用前n项和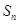 与
与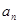 之间的关系
之间的关系 ,令
,令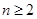 时,
时,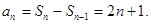 然后验证首项
然后验证首项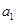 ,即可得到
,即可得到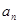 的通项公式.
的通项公式.
(3)把(2)得到的 带入
带入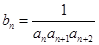 ,即可得到
,即可得到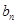 的通项公式,为求其前n项和
的通项公式,为求其前n项和 ,可以把
,可以把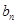 进行裂项
进行裂项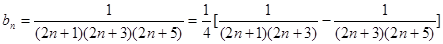 ,进而采用裂项求和的方法即可得到
,进而采用裂项求和的方法即可得到 ,再利用
,再利用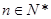 非负即可证明
非负即可证明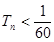
试题解析:
(1)∵点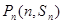 都在函数
都在函数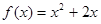 的图象上,
的图象上,
∴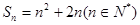 , (1分)
, (1分)
∴ , (2分)
, (2分)
又 ,∴
,∴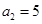 . (4分)
. (4分)
(2)由(1)知,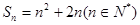 ,
,
当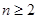 时,
时,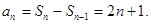 (6分)
(6分)
由(1)知,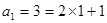 满足上式, (7分)
满足上式, (7分)
所以数列 的通项公式为
的通项公式为 . (8分)
. (8分)
(3)由(2)得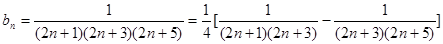 (11分)
(11分)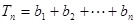
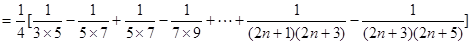 (12分)
(12分) (13分)
(13分)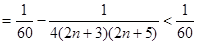 . (14分)
. (14分)
考点:裂项求和 不等式 数列前n项和


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com