
【题目】如图,在多面体![]() 中,
中,![]() 、
、![]() 、
、![]() 均垂直于平面
均垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)求二面角![]() 的大小.
的大小.
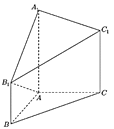
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
由题意建立空间直角坐标系.
(1)由已知分别求出![]() 的坐标与平面A1B1C1 的一个法向量,则线面角可求;
的坐标与平面A1B1C1 的一个法向量,则线面角可求;
(2)求出平面AA1B1 的一个法向量,结合(1),由两法向量所成角的余弦值可得二面角A﹣A1B1﹣C1的大小.
由题意建立如图所示空间直角坐标系,
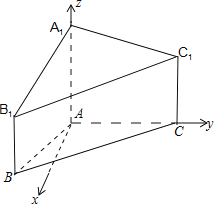
∵AA1=4,CC1=3,BB1=AB=AC=2,∠BAC=120°,
∴A(0,0,0),A1 (0,0,4),B1 (![]() ,﹣1,2),C1 (0,2,3).
,﹣1,2),C1 (0,2,3).
(1)![]() ,
,![]() ,
,![]() ,
,
设平面A1B1C1 的一个法向量为![]() ,
,
由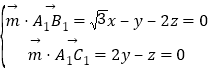 ,取y=1,得
,取y=1,得![]() .
.
∴AB1与A1B1C1所成角的最小值sinθ=|cos![]() |
|![]() .
.
∴AB1与A1B1C1所成角的大小为![]() ;
;
(2)设平面AA1B1 的一个法向量为![]() ,
,
由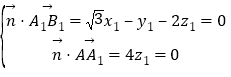 ,取x1=1,得
,取x1=1,得![]() .
.
∴cos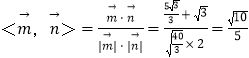 .
.
∴二面角A﹣A1B1﹣C1的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() 分别为
分别为![]() 的中点
的中点![]()
![]() 为
为![]() 中点,现将四边形
中点,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体,在图②中.
,得到如图②所示的多面体,在图②中. 
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,上顶点B是抛物线
,上顶点B是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个动点,且
上的两个动点,且![]() (
(![]() 是坐标原点),试问:点到直线的距离是否为定值?若是,试求出这个定值;若不是,请说明理由.
是坐标原点),试问:点到直线的距离是否为定值?若是,试求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com