
【题目】已知椭圆![]() 的长轴长与焦距分别为方程
的长轴长与焦距分别为方程![]() 的两个实数根.
的两个实数根.
(1)求椭圆的标准方程;
(2)若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() ,
,![]() 两点,
两点,![]() 是椭圆的左焦点,当
是椭圆的左焦点,当![]() 面积最大时,求直线
面积最大时,求直线![]() 的斜率.
的斜率.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】如图,将边长为1的正方形ABCD沿x轴正向滚动,先以A为中心顺时针旋转,当B落在x轴时,又以B为中心顺时针旋转,如此下去,设顶点C滚动时的曲线方程为![]() ,则下列说法不正确的是
,则下列说法不正确的是![]()

A.![]() 恒成立B.
恒成立B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的),绘制散点图发现,可用线性回归模型拟合y与x的关系:
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)某5岁儿童的体重为13.00kg,估测此儿童的体积.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,137×14=1918.00.
,137×14=1918.00.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: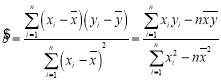 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源于中国古代数学家祖冲之的圆周率。公元263年,中国数学家刘徽用“割圆术”计算圆周率,计算到圆内接3072边形的面积,得到的圆周率是![]() .公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率
.公元480年左右,南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果,给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率![]() 和约率
和约率![]() 。大约在公元530年,印度数学大师阿耶波多算出圆周率约为
。大约在公元530年,印度数学大师阿耶波多算出圆周率约为![]() (
(![]() ).在这4个圆周率的近似值中,最接近真实值的是( )
).在这4个圆周率的近似值中,最接近真实值的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0 (n∈N ),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设![]() ,数列{bn}的前n项和为Sn,当
,数列{bn}的前n项和为Sn,当![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
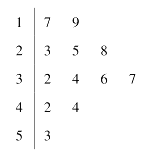
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;当月低于40万件没有奖励,用该样本估计总体,从电商平台一个年度内高于该年月销售平均数的月份中任取两个月,求这两个月企业发给电商平台的奖金为20万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央精准扶贫决策,某市将其低收入家庭的基本情况经过统计绘制如图,其中各项统计不重复.若该市老年低收入家庭共有900户,则下列说法错误的是( )
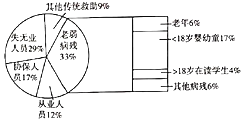
A.该市总有 15000 户低收入家庭
B.在该市从业人员中,低收入家庭共有1800户
C.在该市无业人员中,低收入家庭有4350户
D.在该市大于18岁在读学生中,低收入家庭有 800 户
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.

图一

图二
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com