
 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?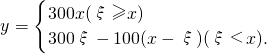
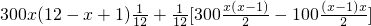 =
=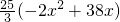 .
.

科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
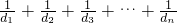 4(n∈N*)5,求Tn;
4(n∈N*)5,求Tn;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,
,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令ξ表示该公司的资助总额.求出ξ数学期望Eξ.
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令ξ表示该公司的资助总额.求出ξ数学期望Eξ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 一年级 | 二年级 | 三年级 | |
| 女生 | 373 | C2 | C1 |
| 男生 | 377 | 370 | C2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com