【题目】一个简单几何体的三视图如图所示，其中正视图是一个正三角形，俯视图是等腰直角三角形，则该几何体的体积为 ， 表面积为 ．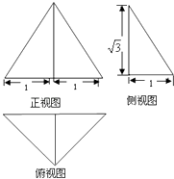 
【答案】
?；
【解析】解：由三视图知：几何体是三棱锥，且几何体的后侧面SAC与底面垂直，高SO为 
， 如图：
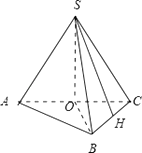
其中OA=OB=OC=1，SO⊥平面ABC，
AB=BC= 
，SA=SB=SC=2，
底面△ABC的面积为： 
，
后侧面△SAC的面积为： 
，
左右两个侧面△SAB和△SBC的底面边长为 ，两腰长为2，
故底边上的高为： 
= 
，
故左右两个侧面△SAB和△SBC的面积为： 
，
故几何体的表面积： ，
几何体的体积V= 
= ，
所以答案是： ，
【考点精析】根据题目的已知条件，利用由三视图求面积、体积的相关知识可以得到问题的答案，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2+2ax+3．
（1）若f（x）在（﹣∞， 
]是减函数，在[ ，+∞）是增函数，求函数f（x）在区间[﹣1，5]的最大值和最小值．
（2）求实数a的取值范围，使f（x）在区间[﹣5，5]上是单调函数，并指出相应的单调性．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知F1 ， F2分别为双曲线C： 
=1的左、右焦点，若存在过F1的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF2=∠BF2F1 ， 则双曲线C的离心率e的取值范围是（ ）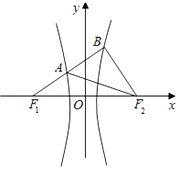 
A.（3，+∞）
B.（1，2+ 
）
C.（3，2+ ）
D.（1，3）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱柱
中， 
平面
， 
， 
， 
，点
在棱
上，且
．建立如图所示的空间直角坐标系．
（1）当
时，求异面直线
与
的夹角的余弦值；
（2）若二面角
的平面角为
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方体ABCD﹣A1B1C1D1的棱长为1，E，F是线段B1D上的两个动点，且EF= 
，则下列结论错误的是（ ） 
A.AC⊥BF
B.直线AE，BF所成的角为定值
C.EF∥平面ABC
D.三棱锥A﹣BEF的体积为定值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥S﹣ABCD中，△ABD是正三角形，CB=CD，SC⊥BD．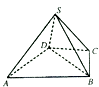 
（Ⅰ）求证：SB=SD；
（Ⅱ）若∠BCD=120°，M为棱SA的中点，求证：DM∥平面SBC．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）是定义在R上的奇函数，当x≤0时，f（x）=x（2+x）．
（1）求函数f（x）的解析式；
（2）画出函数f（x）的图象，并写出单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C1：x2+y2﹣3x﹣3y+3=0，圆C2：x2+y2﹣2x﹣2y=0．
（1）求两圆的公共弦所在的直线方程及公共弦长．
（2）求过两圆交点且面积最小的圆的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
