
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点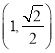 .
.
(1)求椭圆![]() 的方程;
的方程;
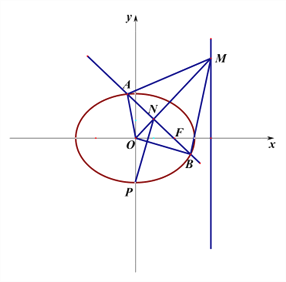
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆几何条件得椭圆四个顶点组成的四边形为菱形,其面积为![]() ,
, ![]() ,又
,又 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,解方程组得
,解方程组得![]() ,
, ![]()
(2)先确定面积计算方法: ![]() ,
, ![]() ,再确定计算方向:设
,再确定计算方向:设![]() ,根据
,根据
两点间距离公式求![]() ,根据两直线交点求
,根据两直线交点求![]() 点横坐标,再根据直线方程与椭圆方程联立方程组,结合韦达定理求弦长
点横坐标,再根据直线方程与椭圆方程联立方程组,结合韦达定理求弦长![]() ,最后根据
,最后根据![]() 表达式形式,确定求最值方法(基本不等式求最值)
表达式形式,确定求最值方法(基本不等式求最值)
试题解析:
(1)因为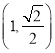 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
又因为椭圆四个顶点组成的四边形的面积为![]() ,所以
,所以![]() ,
,
解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]()
(2) 由(1)可知![]() ,设
,设![]() ,
,
则当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由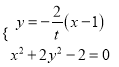 得
得![]() ,
,
则![]() ,
,
![]() ,
,
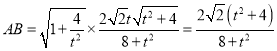 ,
,
又![]() ,所以
,所以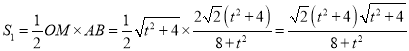 ,
,
由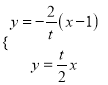 ,得
,得![]() ,所以
,所以![]() ,
,
所以 ,
,
当![]() ,直线
,直线![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以当![]() 时,
时, ![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 写出曲线
写出曲线![]() 的极坐标的方程以及曲线
的极坐标的方程以及曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若过点
若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=16.
(1)若a=4,b=5,求cosC的值;
(2)若sinA+sinB=3sinC,且△ABC的面积S=18sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,关于实数
,关于实数![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)是否存在实数![]() ,使得关于
,使得关于![]() 的函数
的函数![]() (
(![]() )的最小值为
)的最小值为![]() ?若存在,求实数
?若存在,求实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代数学名著《九章算术》中的“盈不足”问题知两鼠穿垣.今有垣厚5尺,两鼠对穿.大鼠日一尺,小鼠亦一尺.大鼠日自倍,小鼠日自半.问:何日相逢?题意是:由垛厚五尺(旧制长度单位, ![]() 尺=
尺= ![]() 寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进
寸)的墙壁,大小两只老鼠同时从墙的两面,沿一直线相对打洞.大鼠第一天打进![]() 尺,以后每天的速度为前一天的
尺,以后每天的速度为前一天的![]() 倍;小鼠第一天也打进
倍;小鼠第一天也打进![]() 尺,以后每天的进度是前一天的一半.它们多久可以相遇?
尺,以后每天的进度是前一天的一半.它们多久可以相遇?
A. ![]() 天 B.
天 B. ![]() 天 C.
天 C. ![]() 天 D.
天 D. ![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n.
(1)画出执行该问题的程序框图;
(2)以下是解决该问题的一个程序,但有2处错误,请找出错误并予以更正.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com