
(2007
四川,19)如下图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1.∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.(1)
求证:平面PAC⊥平面ABC;(2)
求二面角M-AC-B的大小;(3)
求三棱锥P-MAC的体积.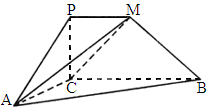
|
解析:解法一: (1)∵PC⊥AB,PC⊥BC, , ,
∴ PC⊥平面ABC.又∵PC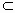 平面PAC, 平面PAC,
∴平面 PAC⊥平面ABC.(2) 取BC的中点N,则CN=1.连结 AN、MN,∵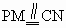 . .
∴ 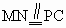 ,从而MN⊥平面ABC. ,从而MN⊥平面ABC.
作 NH⊥AC,交AC的延长线于H,连结MH,则由三垂线定理知,AC⊥MH,从而∠MHN为二面角M-AC-B的平面角.∵直线 AM与直线PC所成的角为60°,∴∠ AMN=60°.在△ ACN中,由余弦定理得
在 Rt△AMN中, .在Rt△CNH中, .在Rt△CNH中,
在 Rt△MNH,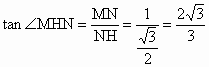 . .
故二面角 M-AC-B的大小为 . .
(3) 由(2)知,PCNM为正方形,
解法二: (1)同解法一.(2) 在平面ABC内,过C作CD⊥CB.建立空间直角坐标系C-xyz(如图),
由题意有 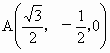 . .
设 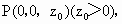 则 则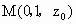 , ,
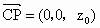 . .
由直线 AM与直线PC所成的角为60°,得 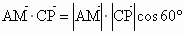 , ,
即  ,解得 ,解得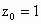 . .
平面 MAC的一个法向量为
则  取 取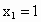 , ,
得 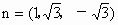 . .
平面 ABC的法向量取为m=(0,0,1).设 m与n所成角为θ,则 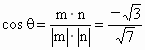 ,显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的大小为 ,显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的大小为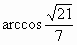 . .
(3) 取平面PCM的法向量为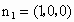 , ,
则点 A到平面PCM的距离 . .
因 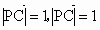 , ,
|


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com