
【题目】如图,正三棱锥![]() ,已知
,已知![]() ,
, ![]()
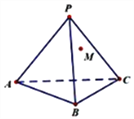
(1)求此三棱锥内切球的半径.
(2)若![]() 是侧面
是侧面![]() 上一点,试在面
上一点,试在面![]() 上过点
上过点![]() 画一条与棱
画一条与棱![]() 垂直的线段,并说明理由.
垂直的线段,并说明理由.
【答案】(1)半径为 ![]() ;(2) 过
;(2) 过![]() 作线段
作线段![]() 平行于
平行于![]() ,则
,则![]() 为所求,证明见解析.
为所求,证明见解析.
【解析】试题分析; (1)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,由正三棱锥的性质可得
,由正三棱锥的性质可得![]() 为底面正三角形的中心,,求解三角形可得
为底面正三角形的中心,,求解三角形可得![]() ,进一步得到
,进一步得到![]() ,求得
,求得![]() ,再由棱锥体积公式求得正三棱锥
,再由棱锥体积公式求得正三棱锥![]() 的体积,最后
的体积,最后![]()
![]() 可求此三棱锥内切球的半径
可求此三棱锥内切球的半径![]() ;
;
(2)由(1)结合线面垂直的判定可得![]() ,得到
,得到![]() ,过
,过![]() 作线段
作线段![]() 平行于
平行于![]() ,则
,则![]() 为所求.
为所求.
试题解析;(1)如图,过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,
∵![]() 为正三棱锥,∴
为正三棱锥,∴![]() 为底面正三角形的中心,
为底面正三角形的中心,
连接![]() 并延长交
并延长交![]() 于
于![]() ,
,
则![]() ,且
,且![]() ,
,
∴![]() ,则
,则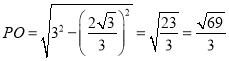 .
.
∴![]()
 ;
;
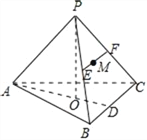
(2)过![]() 作线段
作线段![]() 平行于
平行于![]() ,则
,则![]() 为所求.
为所求.
理由:∵![]() 为正三棱锥,
为正三棱锥,
过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,
∴![]() 为底面正三角形的中心,
为底面正三角形的中心,
则![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知某渔船在渔港O的南偏东60°方向,距离渔港约160海里的B处出现险情,此时在渔港的正上方恰好有一架海事巡逻飞机A接到渔船的求救信号,海事巡逻飞机迅速将情况通知了在C处的渔政船并要求其迅速赶往出事地点施救.若海事巡逻飞机测得渔船B的俯角为68.20°,测得渔政船C的俯角为63.43°,且渔政船位于渔船的北偏东60°方向上.
(Ⅰ)计算渔政船C与渔港O的距离;
(Ⅱ)若渔政船以每小时25海里的速度直线行驶,能否在3小时内赶到出事地点?
(参考数据:sin68.20°≈0.93,tan68.20°≈2.50,shin63.43°≈0.90,tan63.43°≈2.00, ![]() ≈3.62,
≈3.62, ![]() ≈3.61)
≈3.61)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“茭草形段”第一个问题“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.问底子(每层三角形边茭草束数,等价于层数)几何?”中探讨了“垛枳术”中的落一形垛(“落一形”即是指顶上1束,下一层3束,再下一层6束,…,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层茭草束数),则本问题中三角垛底层茭草总束数为 .
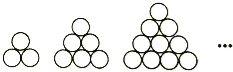
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,先将梯形
,先将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点. 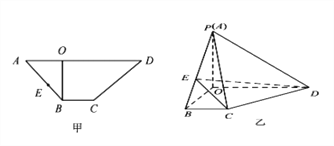
(1)证明: ![]() ;
;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.
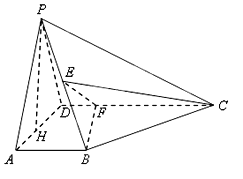
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
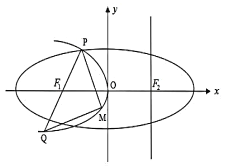
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com