Question

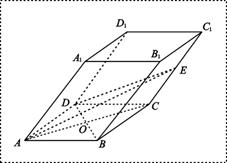
（满分14分）在斜四棱柱中，已知底面是边长为4的菱形，，且点在面上的射影是底面对角线与AC的交点O，设点E是的中点，．

   （Ⅰ） 求证：四边形是矩形；

   （Ⅱ） 求二面角的大小；

   （Ⅲ） 求四面体的体积．[来源:学科网]

Answer 1

（I）略    （Ⅱ）     （Ⅲ）

解析:

解法一：（Ⅰ） 连接．

因为四边形为菱形，

所以,又面，[所以．

而，所以．因为四边形是平行四边形，所以四边形是矩形．[来源:学,科,网]

   （Ⅱ） 连接OE，因为,所以平面，∴ ,即为二面角

E──C的平面角．在菱形中， 

又E是的中点，．所以．[来源:Zxxk.Com]

在△中，,[来源:Z。xx。k.Com]∴ ，,[来源:学科网]

所以在△中，有，即二面角E─BD─C的大小为．      9分

   （Ⅲ） 设点D到平面的距离为h，则有．

因为是的中点，所以14分

解法二：（Ⅰ） 连结AC、BD相交于O，连结．

由已知，有AC⊥BD，⊥面ABCD，故可建立空间直角坐标系，

且以下各点的坐标分别为：，  1分

设, ， 3分又, 四边形为平行四边形．是矩形． 4分

   （Ⅱ） 设,则．

， 由 可求得

∴． 设为平面EBD的法向量，

则由，得

可取 , ． 6分

平面平面BDC的法向量为，

而 ． 

∴ 二面角E─BD─C的大小为．    9分

   （Ⅲ） 设为平面的法向量，

则由 ,得

∴ 可取，．

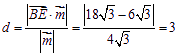到平面的距离 ．    11分  

而，又由（Ⅰ）知， ，

．················ 14分