
【题目】若存在实数![]() ,对任意实数
,对任意实数![]() ,使不等式
,使不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
不等式![]() 可化为不等式
可化为不等式![]() ,等价于存在实数a,b,对任意
,等价于存在实数a,b,对任意![]() ,不等式
,不等式![]() 成立,等价于存在实数a,b,不等式
成立,等价于存在实数a,b,不等式![]() 成立,分别讨论
成立,分别讨论![]() ,
,![]() ,
,![]() 的情况,注意由任意性和存在性可知需先求出
的情况,注意由任意性和存在性可知需先求出![]() ,再求
,再求![]() 即可解决.
即可解决.
不等式![]() 可化为不等式
可化为不等式![]() ,
,
原题等价于存在实数a,b,对任意![]() ,不等式
,不等式![]() 成立,
成立,
等价于存在实数a,b,不等式![]() 成立,
成立,
令![]() ,则
,则![]() ,
,
(1)在![]() 上,当
上,当![]() ,即
,即![]() 时,函数单调递减,
时,函数单调递减,
此时![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() ,则
,则![]() ,
,
从而当![]() 时,设
时,设![]() ,
,
则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;
;
(2)当![]() 时,由
时,由![]() 可得,y在
可得,y在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
①在![]() 时,
时,![]() ,则
,则![]() ,
,
同理可得,当![]() 时,
时,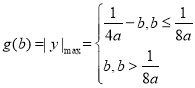 ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,故当
单调递增,故当![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;
;
②在![]() 时,
时,![]() ,则
,则![]() ,
,
同理可得,当![]() 时,
时,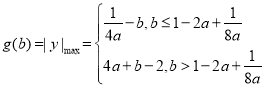 ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故当![]() 时,
时,![]() 取最小值,最小值为
取最小值,最小值为![]() ,
,
根据对勾函数的性质可得,![]() .
.
综上所述,![]() ,即
,即![]() ,
,![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某家报刊销售点从报社买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以每份0.08元的价格退回报社.在一个月(30天)里,有20天每天可以卖出400份,其余10天每天只能卖出250份.设每天从报社买进的报纸的数量相同,则应该每天从报社买进多少份,才能使每月所获得的利润最大?并计算该销售点一个月最多可赚得多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第1组 | [90,100) | 15 | ① |
第2组 | [100,110) | ② | 0.35 |
第3组 | [110,120) | 20 | 0.20 |
第4组 | [120,130) | 20 | 0.20 |
第5组 | [130,140) | 10 | 0.10 |
合计 | 100 | 1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,多个区间并集的长度为各区间长度之和,例如,
,多个区间并集的长度为各区间长度之和,例如, ![]() 的长度
的长度![]() . 用
. 用![]() 表示不超过
表示不超过![]() 的最大整数,记
的最大整数,记![]() ,其中
,其中![]() .设
.设![]() ,
,![]() ,当
,当![]() 时,不等式
时,不等式![]() 解集区间的长度为
解集区间的长度为![]() ,则
,则![]() 的值为
的值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上单调递增,在区间
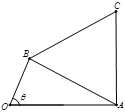
上单调递增,在区间![]() 上单调递减;如图,四边形
上单调递减;如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的内角
的内角![]() 的对边,
的对边,
且满足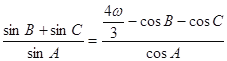 .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,设
,设![]() ,
,![]() ,
,
![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过坐标原点的直线l与圆C:x2+y2﹣8x+12=0相交于不同的两点A,B.
(1)求线段AB的中点P的轨迹M的方程.
(2)是否存在实数k,使得直线l1:y=k(x﹣5)与曲线M有且仅有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.哪种购物方式比较经济?你能把所得结论作一些推广吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若对定义域内的任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的值;
的值;
(2)若函数![]() 的定义域上是单调函数,求实数
的定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意的正整数
,证明对任意的正整数![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com