【题目】设奇函数
上是增函数，且
，则不等式
的解集为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
本题考查的是函数的奇偶性和单调性以及解不等式的综合类问题．在解答时，首先要结合奇偶性和单调性对不等式进行转化变形，将问题转化为解不等式：2xf（x）＜0，
然后再分类讨论即可获得问题的解答．
：∵函数f（x）是奇函数，函数f（x）在（0，+∞）上是增函数，
∴它在（-∞，0）上也是增函数．∵f（-x）=-f（x），
∴f（-1）=f（1）=0．
不等式x[f（x）-f（-x）]＜0可化为2xf（x）＜0，
即xf（x）＜0，
∴当x＜0时，
可得f（x）＞0=f（-1），∴x＞-1，
∴-1＜x＜0；
当x＞0时，可得f（x）＜0=f（1），
∴x＜1，∴0＜x＜1．
综上，不等式x[f（x）-f（-x）]＜0的解集为{x|-1＜x＜0，或0＜x＜1}．
故选：D．
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案科目：高中数学 来源： 题型：
【题目】某服装厂生产一种服装，每件服装成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，规定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低
元，根据市场调查，销售商一次订购不会超过600件.
（1）设一次订购
件，服装的实际出厂单价为
元，写出函数
的表达式；
（2）当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知AB是⊙O的直径，直线AF交⊙O于F（不与B重合），直线EC与⊙O相切于C，交AB于E，连接AC，且∠OAC=∠CAF，求证：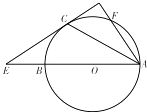 
（1）AF⊥EC；
（2）若AE=5，AF=2，求AC．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中， 
所对的边分别为
，且
.
(1)求角
的大小；
(2)若
， 
， 
为
的中点，求
的长．
【答案】（1）
；（2）
.
【解析】试题分析：（1）由已知，利用正弦定理可得
a2＝
b2＋
c2－2b，再利用余弦定理即可得出cosA，结合A的范围即可得解A的值．
（2）△ABC中，先由正弦定理求得AC的值，再由余弦定理求得AB的值，△ABD中，由余弦定理求得BD的值．
试题解析：
(1)因为
asin A＝(b－c)sin B＋(c－b)·sin C，
由正弦定理得a2＝(b－c)b＋(c－b)c，
整理得a2＝c2－2bc，
由余弦定理得cos A＝
＝
＝
，
因为A∈(0，π)，所以A＝
.
(2)由cos B＝
，得sin B＝
＝
＝
，
所以cos C＝cos[π－(A＋B)]＝－cos(A＋B)＝－
＝－
，
由正弦定理得b＝
＝
＝2，
所以CD＝
AC＝1，
在△BCD中，由余弦定理得BD2＝(
)2＋12－2×1××
＝13，
所以BD＝
.
【题型】解答题
【结束】
21
【题目】已知函数
在
处的切线经过点
（1）讨论函数
的单调性；
（2）若不等式
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】①在同一坐标系中，
与
的图象关于
轴对称；
②
是奇函数；
③
的图象关于
成中心对称；
④
的最大值为
；
⑤
的单调增区间：
。
以上五个判断正确有____________________（写上所有正确判断的序号）。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
给出下列四个命题：
①c = 0时，
是奇函数； ②
时，方程
只有一个实根；
③的图象关于点(0 , c)对称； ④方程至多3个实根.
其中正确的命题个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的离心率为
，以原点为圆心，椭圆的短半轴长为半径的圆与直线
相切. 
、
是椭圆
的右顶点与上顶点，直线
与椭圆相交于
、
两点.
（Ⅰ）求椭圆
的方程；
（Ⅱ）当四边形
面积取最大值时，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=ex（ax2﹣x﹣1）（a∈R）．
（1）若函数f（x）在R上单调递减，求a的取值范围
（2）当a＞0时，求f（|sinx|）的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍，再横坐标不变纵坐标伸长到原来的2倍，最后向右平移
个单位而得到.
⑴求f(x)的解析式与最小正周期；
⑵求f(x)在x∈(0，π)上的值域与单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com