
【题目】已知椭圆![]() 过点
过点![]() ,且左焦点与抛物线
,且左焦点与抛物线![]() 的焦点重合。
的焦点重合。
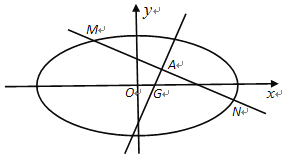
(1)求椭圆的标准方程;
(2)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,线段
,线段![]() 的中点记为
的中点记为![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围。
的取值范围。
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由左焦点与抛物线的焦点重合,可以求得c,再利用椭圆过点![]() 求得
求得![]() 、
、![]() ,从而求出椭圆方程。
,从而求出椭圆方程。
(2)由直线与椭圆交于不同的两点,可以由![]() 得到k与m的不等关系,再由AG直线与
得到k与m的不等关系,再由AG直线与![]() 直线垂直,斜率乘积为-1,得到k与m的等量关系,将等量关系代入不等关系来限定k的取值范围。
直线垂直,斜率乘积为-1,得到k与m的等量关系,将等量关系代入不等关系来限定k的取值范围。
(1)〖解法1〗![]() 抛物线
抛物线![]() 的焦点为F(-1,0),
的焦点为F(-1,0),
依题意知,椭圆的左右焦点坐标分别为![]() ,
,![]()
又椭圆过点![]() ,∴由椭圆的定义知,
,∴由椭圆的定义知,![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]()
∴椭圆的方程为![]() .
.
(1)〖解法2〗![]() 抛物线
抛物线![]() 的焦点为F(-1,0),
的焦点为F(-1,0),
依题意知,椭圆的左右焦点坐标分别为![]() ,
,![]()
又椭圆过点![]() ,∴
,∴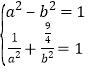
解得![]() ,
,![]()
∴椭圆的方程为![]() .
.
(1)〖解法3〗![]() 抛物线
抛物线![]() 的焦点为F(-1,0),
的焦点为F(-1,0),
依题意知,椭圆的左右焦点坐标分别为![]() ,
,![]()
又椭圆过点![]() ,∴
,∴![]()
∴![]() ,∵
,∵![]()
∴可解得![]() ,
,![]()
∴椭圆的方程为![]() .
.
(2)〖解法1〗由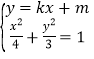 消去
消去![]() 整理得
整理得
![]() ,
,
![]() 直线与椭圆交于不同的两点,
直线与椭圆交于不同的两点,
![]() ,整理得
,整理得![]() ……①
……①
设![]() ,线段
,线段![]() 的中点A
的中点A![]() ,
,
则![]() ,
,
∴![]() ∴
∴![]() ,
,
∴点A的坐标为![]() ,
,
∴直线AG的斜率为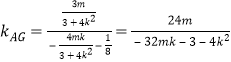 ,
,
又直线AG和直线MN垂直,
∴![]() ,∴
,∴![]() ,
,
将上式代入①式,可得![]() ,
,
整理得![]() ,解得
,解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.
(2)〖解法2〗设![]()
则![]()
![]() 两式相减得
两式相减得
![]() 即
即 ![]()
![]() 点
点![]() 满足方程
满足方程![]() ①.
①.
又![]() 直线
直线![]() 且过点
且过点![]()
![]() 点
点![]() 也满足方程
也满足方程![]() ②
②
联立①②解得![]() ,即
,即![]()
![]() 点
点![]() 在椭圆内部
在椭圆内部![]()
![]()
![]()
![]()
![]()
![]()
![]() 的取值范围为
的取值范围为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(1)用篱笆围一个面积为![]() 的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
的矩形菜园,当这个矩形的边长为多少时,所用篱笆最短?最短篱笆的长度是多少?
(2)用一段长为![]() 的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
的篱笆围成一个矩形菜园,当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上,每隔30分钟抽一包产品,称其重量是否合格,分别记录抽查数据如下(单位:千克):
甲车间:102,101,99,98,103,98,99.
乙车间:110,115,90,85,75,115,110.
(1)这种抽样方式是何种抽样方法;
(2)试根据这组数据说明哪个车间产品较稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
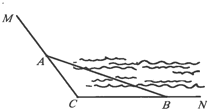
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)那么方程![]() 在区间
在区间![]() 上的根的个数是___________.
上的根的个数是___________.
(2)对于下列命题:
①函数![]() 是周期函数;
是周期函数;
②函数![]() 既有最大值又有最小值;
既有最大值又有最小值;
③函数![]() 的定义域是
的定义域是![]() ,且其图象有对称轴;
,且其图象有对称轴;
④在开区间![]() 上,
上,![]() 单调递减.
单调递减.
其中真命题的序号为______________(填写真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com